Jasmin Patry

Sucker Punch Productions

in

Samurai Shading

Introduction

Sucker Punch is a part of Sony Interactive Entertainment Worldwide Studios (soon PlayStation Studios)
Peak size: 160 people (including 25 QA)
Previous games include:
- Sly Cooper (1, 2, & 3)
- Infamous (1, 2, Festival of Blood, Second Son, First Light)

Introduction

Recently released Ghost of Tsushima for the PlayStation 4

Our goals after Infamous: Second Son and First Light included improving the quality of our materials and lighting
- Particularly for characters
Goal: Support new types of materials, including:
- Materials with strong anisotropic specular response
- Materials with strong asperity scattering component
Goal: Improve fidelity of skin shading
Goal: Make it easy to use detail maps based on scanned materials
- For all types of maps (albedo, gloss, specular, normal, etc.)

Introduction | Goals

Art direction called for “stylized realism”
Lighting models are physically based
Materials authored with physically plausible values, some photogrammetry
Lighting can deviate from physical correctness
- Artists can globally adjust to achieve desired look

Introduction | Lighting

Most lighting in Ghost is deferred:
- Lambertian diffuse
  - Optional translucency
  - Optional simplified asperity scattering (fuzziness)
- Isotropic GGX specular
  - Optional colored specular via “metallic” channel
Other materials are forward lit, e.g. when using:
- Anisotropic GGX specular
- Full anisotropic asperity scattering BRDF
- Subsurface scattering

Introduction | Lighting

Introduction | Overview

This talk is divided into the following four topics:
- Anisotropic specular maps and filtering
- Anisotropic asperity scattering BRDF
- Skin shading improvements
- Physically based detail maps (as bonus slides)

Anisotropic Specular

In previous games, we supported GGX anisotropic specular aligned with mesh tangent space
Wanted to support arbitrary spatially varying orientation
- Plus normal variance filtering
The SGGX paper by Heitz et al. (2015) gave us ideas on ways to accomplish both goals

Anisotropic Specular| Previous Work

LEAN Mapping (Olano and Baker, 2010)
- Uses a Beckmann-like NDF
- Requires choice of scale factor for texture storage
  - 16-bit textures preferable
- For flat normals, gives equivalent results to our algorithm
- Can be adapted to work with GGX-based BRDFs using:
  - \(\sigma\): Beckmann roughness
  - This is the approach that we used in the following comparisons

\sigma = \frac{1}{\sqrt{2}} \alpha

Anisotropic Specular| Previous Work

LEADR Mapping (Dupuy, Heitz, et al., 2013)
- Incorporates displacement mapping
- Accounts for entire BRDF:
  - NDF
  - Masking-shadowing
  - Diffuse microfacets
- Uses Beckmann NDF, and same storage and NDF filtering as LEAN
- Similar to our approach, except that we're:
  - Using the GGX NDF and associated shadow-masking term
  - Using SGGX-based filtering instead of Beckmann-based
  - Not including diffuse microfacets or displacement mapping

Anisotropic Specular | SGGX Recap

SGGX developed as a microflake distribution
- Extends GGX NDF to spherical domain
- NDF of ellipsoid
- GGX is a special case of SGGX

Anisotropic Specular | SGGX Recap

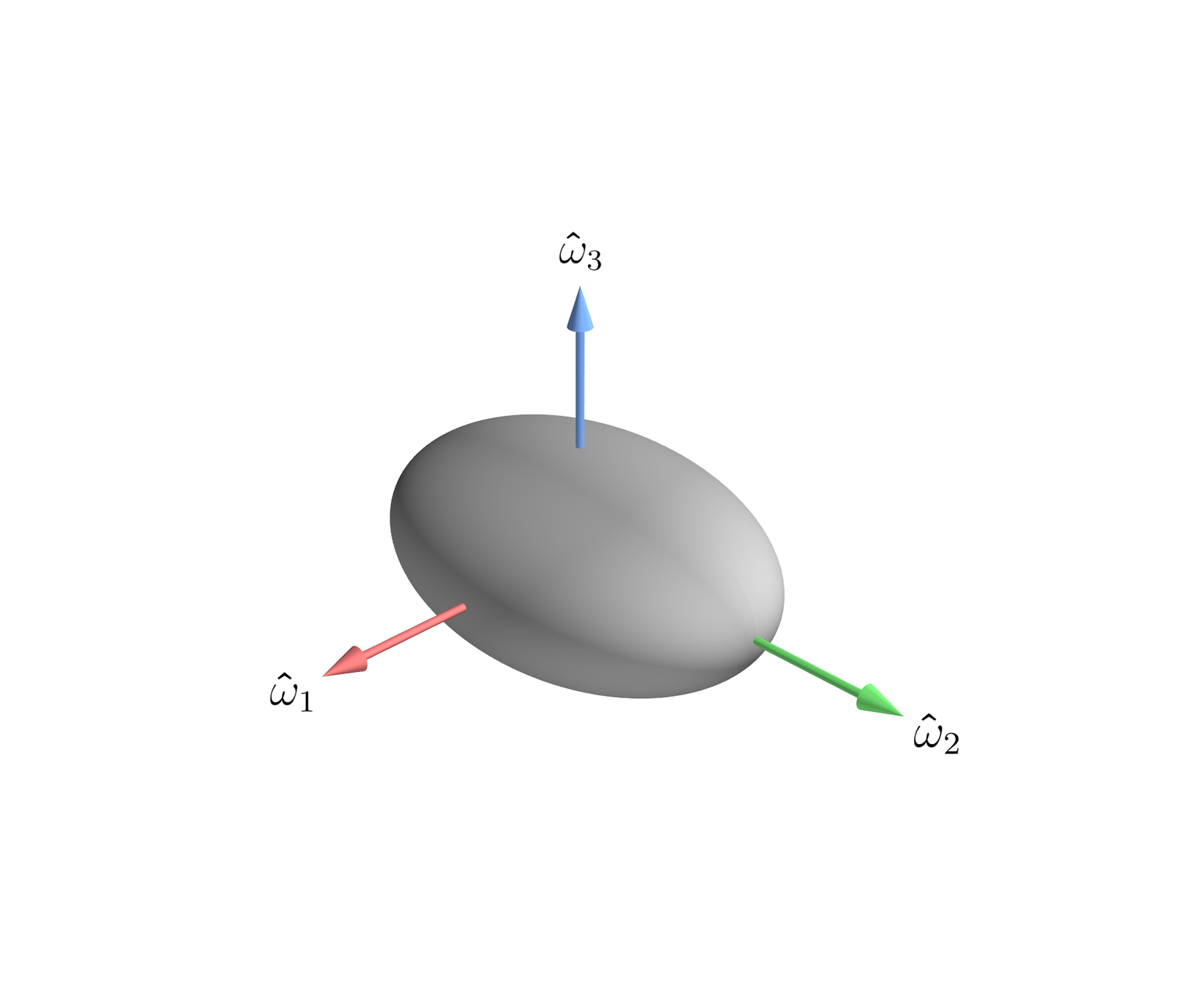
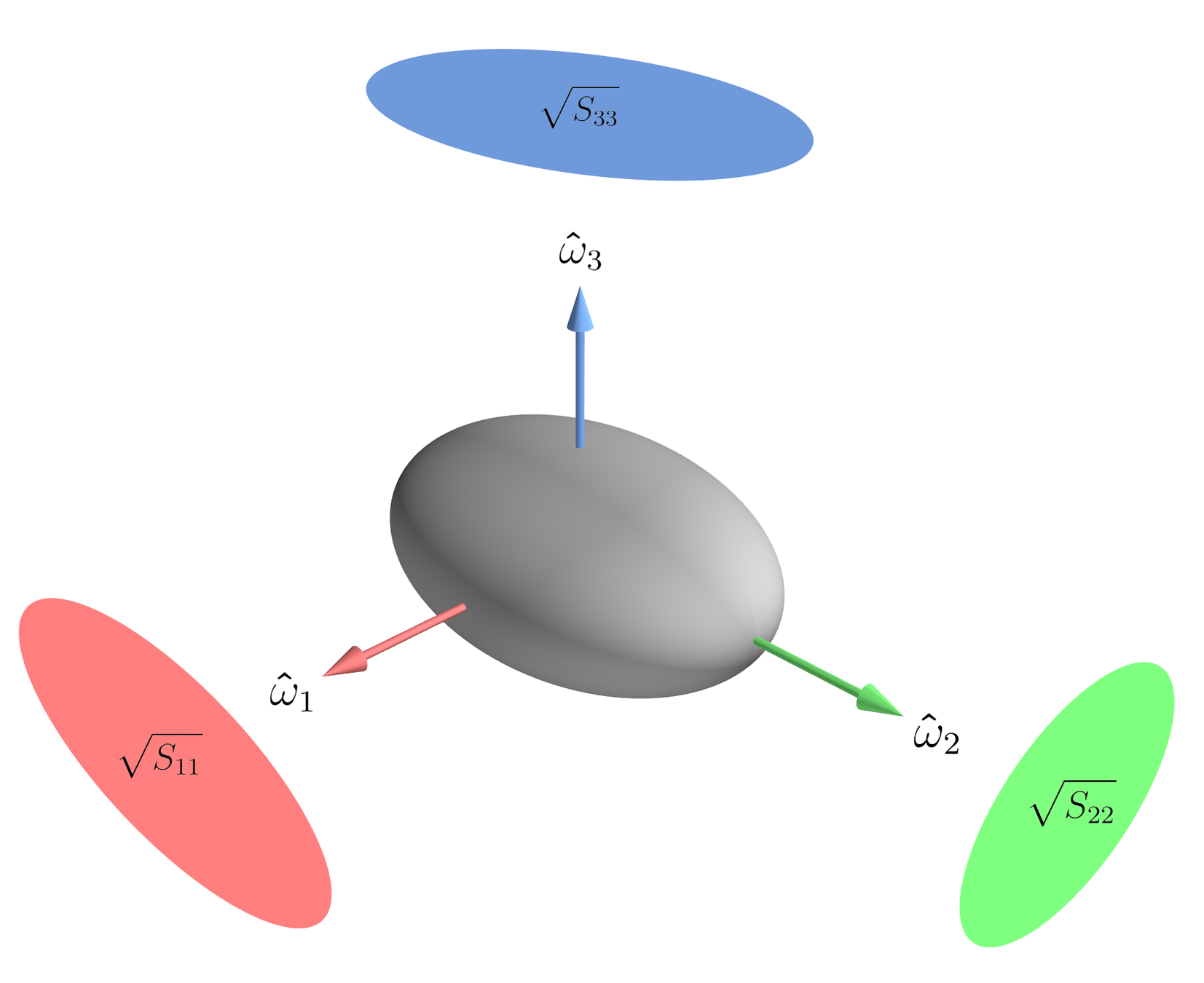
SGGX characterized by an \(\mathbf{S}\) matrix

\(\mathbf{\hat{\omega}}_i\): principal axes of ellipsoid
- Also eigenvectors of \(\mathbf{S}\)
\(S_{ii}\): Square of ellipsoid projected area
- Eigenvalues of \(\mathbf{S}\)

Anisotropic Specular | SGGX Recap

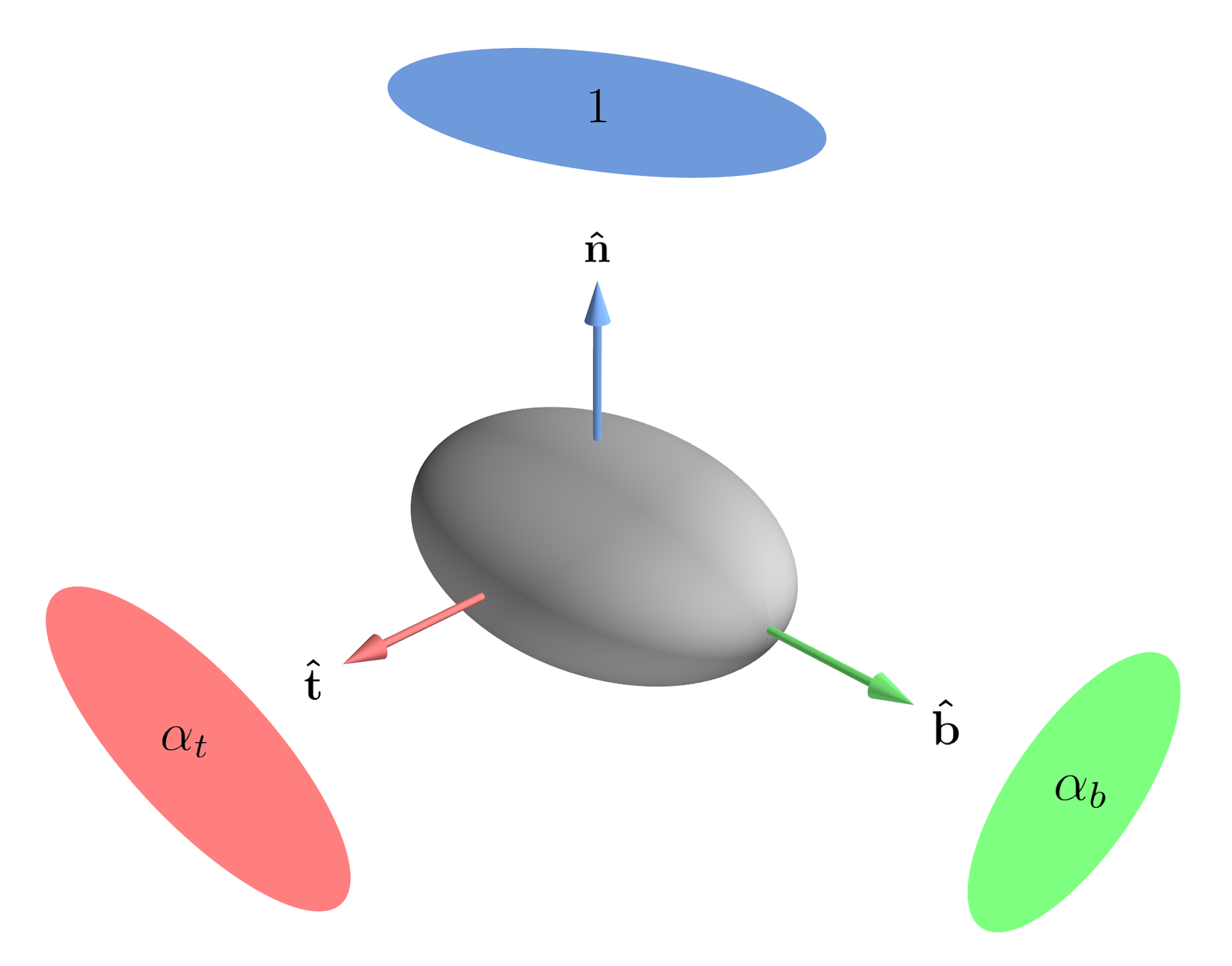
GGX is a special case:

\(\mathbf{\hat{t}}\): Tangent
\(\mathbf{\hat{b}}\): Bitangent
\(\mathbf{\hat{n}}\): Normal
\(\alpha\): GGX roughness

Anisotropic Specular | SGGX Recap

Using the normal-mapped basis defined by \(\mathbf{\hat{t}}_n\), \(\mathbf{\hat{b}}_n\), and \(\mathbf{\hat{n}}\), GGX can also be written as:

\newcommand{\Vector}[1]{\mathbf{#1}} \newcommand{\Normal}[1]{\mathbf{\hat{#1}}} \newcommand{\Color}[1]{\Vector{c}_{#1}} \newcommand{\Lum}[1]{L_{#1}} \newcommand{\Ld}[1]{L_{d,#1}} \newcommand{\Ls}[1]{L_{s,#1}} \newcommand{\Irr}[1]{E_{#1}} \newcommand{\diff}[1]{\, \text{d}#1} \newcommand{\zwsp}[0]{\hspace{0pt}} \newcommand{\V}[0]{\Vector{\hat{v}}} \newcommand{\U}[0]{\Vector{\hat{u}}} \renewcommand{\N}[0]{\Vector{\hat{n}}} \newcommand{\W}[0]{\Vector{\hat{\omega}}} \newcommand{\T}[0]{\Vector{\hat{t}}} \newcommand{\B}[0]{\Vector{\hat{b}}} \newcommand{\h}[0]{\Vector{\hat{h}}} \renewcommand{\S}[0]{\Vector{S}} \Vector{S} = \left[\T_n, \B_n, \N \right] \begin{bmatrix} S_{xx} & S_{xy} & 0\\ S_{xy} & S_{yy} & 0\\ 0 & 0 & 1 \end{bmatrix} \left[\T_n, \B_n, \N \right]^T

\(\mathbf{\hat{t}}_n\): Normal-mapped tangent
\(\mathbf{\hat{b}}_n\): Normal-mapped bitangent
\(\mathbf{\hat{n}}\): Normal-mapped normal
\(S_{xx}, S_{xy}, S_{yy}\): 2x2 GGX submatrix

Anisotropic Specular | SGGX Recap

The SGGX paper describes a “parameter estimation” algorithm for determining the SGGX NDF from an arbitrary NDF
- SGGX NDF ellipsoid has same axes as covariance eigenvectors
- Preserves microflake projected area along these axes
Heitz et al. also show that linearly filtering \(\mathbf{S}\) is a good approximation to this algorithm

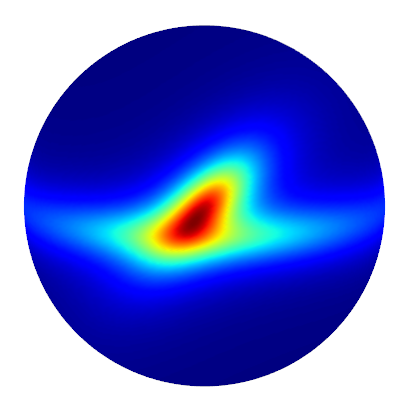
Input NDF

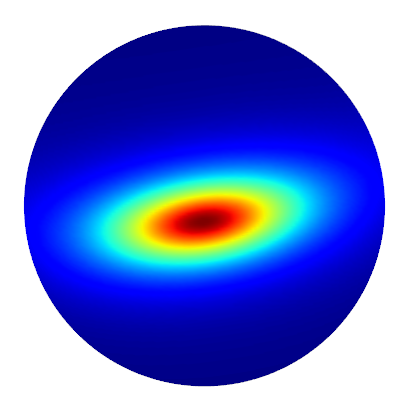
Parameter Estimation

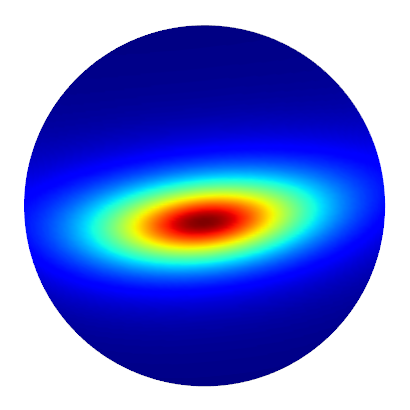
Linear Filtering

Parameter Estimation

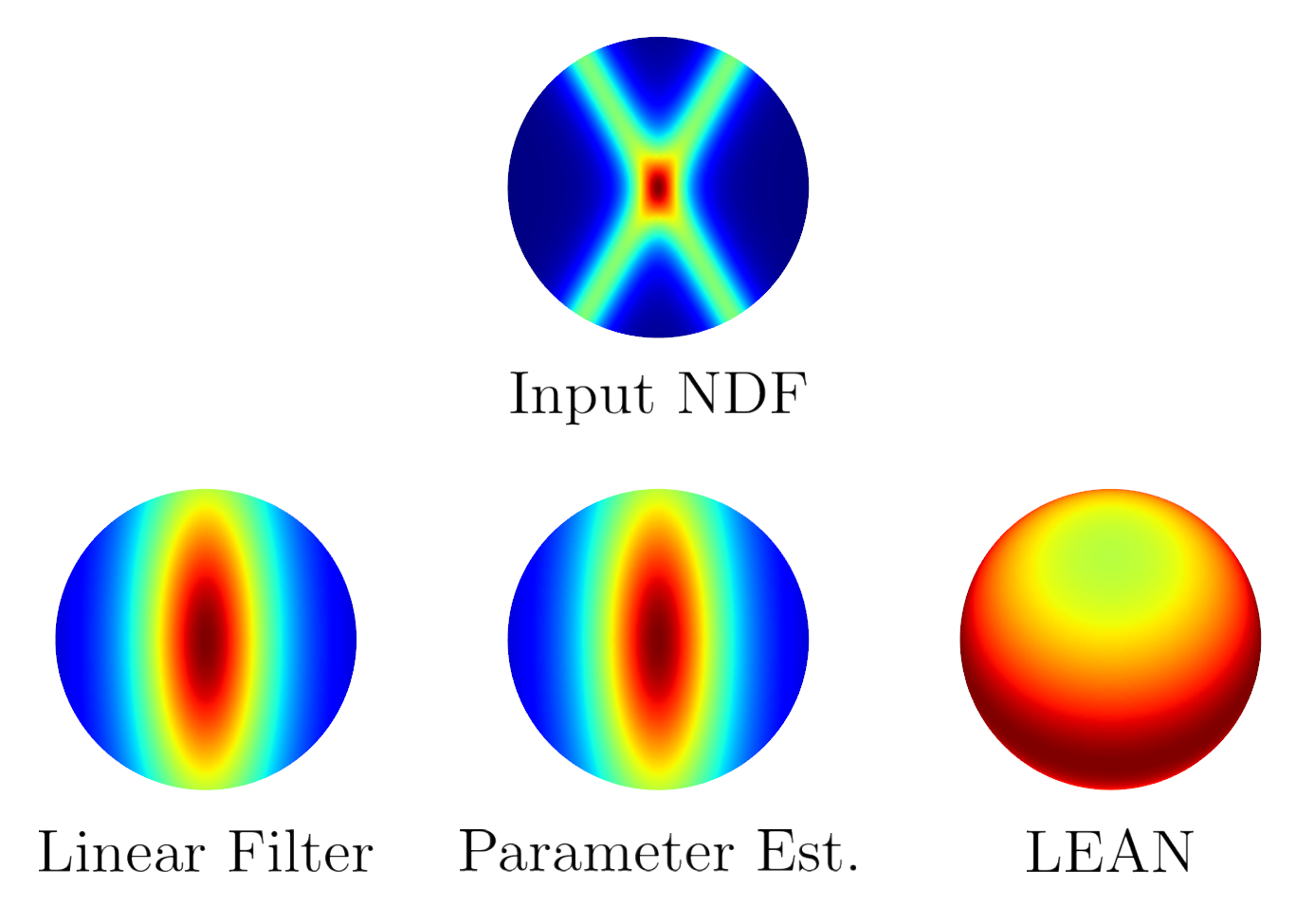
Convert normal + 2x2 anisotropic GGX matrix to 3x3 SGGX matrix \(\mathbf{S}\):

Anisotropic Specular| Our Algorithm

where \(\mathbf{M}_\mathbf{\hat{n}}\) rotates \(\mathbf{\hat{k}}=\left(0, 0, 1\right)\) onto \(\mathbf{\hat{n}} = \left(x, y, z\right)\):

Linearly filter \(\mathbf{S}\) matrices during mipmap generation
Extract new normal \(\mathbf{\hat{n}}'\) and symmetric 2x2 submatrix from new \(\mathbf{S}'\) matrix:

Anisotropic Specular| Our Algorithm

To extract \(\mathbf{\hat{n}}'\) from \(\mathbf{S}'\), use power iteration:

Store to BC5 normal map + BC7 anisotropic specular (“aniso”) map with components

Anisotropic Specular| Our Algorithm

Decode at run time
- One caveat is that linear interpolation of our texture may result in a non-positive definite matrix
  - I.e., negative eigenvalues
- Need to guard against this before using
- We chose to extract the eigenvalues and eigenvectors
  - Need the new anisotropic tangent and bitangent for our ambient specular approximation
- Extract \(\alpha_t^2\), \(\alpha_b^2\), \(\alpha_t\alpha_b\), \(\mathbf{\hat{t}}\), \(\mathbf{\hat{b}}\) for use in:

Anisotropic Specular| Our Algorithm

void DecodeSggx(float3 anisoTex, float3 tangent, float3 bitangent, out SAnisoSpecData anid)
{
    const float s_alphaMin = GgxAlphaFromGloss(1.0f);

    float sxx = Square(anisoTex.x);
    float sxy = anisoTex.x * (anisoTex.y * 2.0 - 1.0) * anisoTex.z;
    float syy = Square(anisoTex.z);

    float discr = sqrt(4.0f * Square(sxy) + Square(sxx - syy));
    float discrRcp = rcp(max(discr, 1e-6f));

    anid.m_alphaTSqr = max(saturate(0.5f * (sxx + syy + discr)), Square(s_alphaMin));
    anid.m_alphaBSqr = max(saturate(0.5f * (sxx + syy - discr)), Square(s_alphaMin));
    anid.m_alphaTB = sqrt(anid.m_alphaTSqr * anid.m_alphaBSqr);

    float cSqr = saturate(0.5f * ((sxx - syy) * discrRcp + 1.0f));
    float c = sqrt(cSqr);
    float s = Sign(sxy) * sqrt(1.0f - cSqr);

    anid.m_tangent = c * tangent + s * bitangent;
    anid.m_bitangent = -s * tangent + c * bitangent;
}

Aniso maps are authored by artists using a custom Substance Designer node

Anisotropic Specular| Authoring

Gloss U

Gloss V

Direction

Aniso

Comparison of SGGX and LEAN filtering

Anisotropic Specular| Results

Ground Truth (256 samples per pixel)

SGGX (ours)

LEAN

Ground Truth (256 samples per pixel)

SGGX (ours)

LEAN

Due to encoding, texture hardware does not interpolate \(\mathbf{S}\) matrix directly, which may result in artifacts
- In practice, for real-world materials, this did not result in problems
Combinations of large and small \(\alpha_t\) and \(\alpha_b\) values do not work well

Anisotropic Specular| Limitations

\(\alpha_t = 0.29, \alpha_b = 0.04\)

\(\alpha_t = 0.87, \alpha_b = 0.04\)

\(\alpha_t = 0.87, \alpha_b = 0.1\)

New SGGX-based filtering approach
- Simple to implement
- Same number of parameters (5) as LEAN
- Same/similar shading cost
- Good results for strong normals and highly anisotropic NDFs
New anisotropic roughness texture encoding
- Based on SGGX encoding
- Works well with BC7 compression
  - 1/4 to 1/8th the size of LEAN encoding

Anisotropic Specular| Summary

Anisotropic Asperity Scattering

Anisotropic

Asperity scattering
- ... AKA sheen
- ... AKA fuzziness
- ... AKA fuzz

Asperity Scattering BRDF

Anisotropic

Asperity scattering
- ... AKA sheen
- ... AKA fuzziness
- ... AKA fuzz

Asperity Scattering BRDF

Fuzz

Anisotropic

Asperity scattering
- ... AKA sheen
- ... AKA fuzziness
- ... AKA fuzz

Asperity Scattering BRDF

Fuzz

Anisotropic

Asperity Scattering BRDF

Fuzz

Asperity scattering
- ... AKA sheen
- ... AKA fuzziness
- ... AKA fuzz
New BRDF was researched during look development

Anisotropic

Asperity scattering
- ... AKA sheen
- ... AKA fuzziness
- ... AKA fuzz
New BRDF was researched during look development
Realistic velvet, including crushed velvet, was important at the time
In Ghost, used for moss, felt, horse coats, and some cloth.

Asperity Scattering BRDF

Fuzz

Anisotropic Fuzz | Previous Work

Our old model was ad hoc: Fresnel-like term + wrap lighting
Neubelt & Pettineo (Ready at Dawn) presented their model in this course in 2013
- Uses microfacet framework
- Energy conserving
The Secret of Velvety Skin (Koenderink and Pont, 2002)
- Models fuzziness as a thin single-scattering layer
No existing models supported anisotropy, to our knowledge

Anisotropic Fuzz | New Model

Our new model was inspired by Koenderink and Pont's model
Extended to support:
- Anisotropy
- Shadowing of base layer
- Spherical harmonic lighting

\(\mathbf{\hat{u}}\): Light direction
\(\mathbf{\hat{v}}\): View direction
\(p(\mathbf{\hat{u}}, \mathbf{\hat{v}})\): Phase function
\(\Delta\): Thickness of scattering layer
\(\lambda\): Mean free path
\(d = \frac{\Delta}{\lambda} \ll 1\): Density

Base Layer

Scattering Layer

\Delta

\mathbf{\hat{n}}

\mathbf{\hat{u}}

\mathbf{\hat{v}}

p(\mathbf{\hat{u}}, \mathbf{\hat{v}})

Anisotropic Fuzz | New Model

Koenderink and Pont show that the BRDF of the scattering layer is:

Base Layer

Scattering Layer

\Delta

\mathbf{\hat{n}}

\mathbf{\hat{u}}

\mathbf{\hat{v}}

p(\mathbf{\hat{u}}, \mathbf{\hat{v}})

\(\mathbf{\hat{u}}\): Light direction
\(\mathbf{\hat{v}}\): View direction
\(p(\mathbf{\hat{u}}, \mathbf{\hat{v}})\): Phase function
\(\Delta\): Thickness of scattering layer
\(\lambda\): Mean free path
\(d = \frac{\Delta}{\lambda} \ll 1\): Density
\(\mathbf{c}_f\): Albedo

Isotropic case:

Strongly dependent on view direction

Anisotropic Fuzz | New Model

Anisotropic Fuzz | Velvet Scattering

According to Koenderink and Pont, the scattering diagram for black velvet resembles:

Anisotropic Fuzz | Velvet Scattering

According to Koenderink and Pont, the scattering diagram for black velvet resembles:

Strong back scattering lobe
Smaller forward scattering lobe
Can we find a phase function that reproduces this?

Anisotropic Fuzz | Phase Function

Starting with the Schlick approximation to the Henyey-Greenstein phase function:
- \(k\): asymmetry parameter
Make it dependent on the angle between the half vector \(\mathbf{\hat{h}}\) and the fiber direction \(\mathbf{\hat{t}}\):
- \(r(k)\): normalization factor (approximate and conservative)

Anisotropic Fuzz | Phase Function

Using this function in the BRDF, we get:

... which is qualitatively similar, at least.

Anisotropic Fuzz | Phase Function

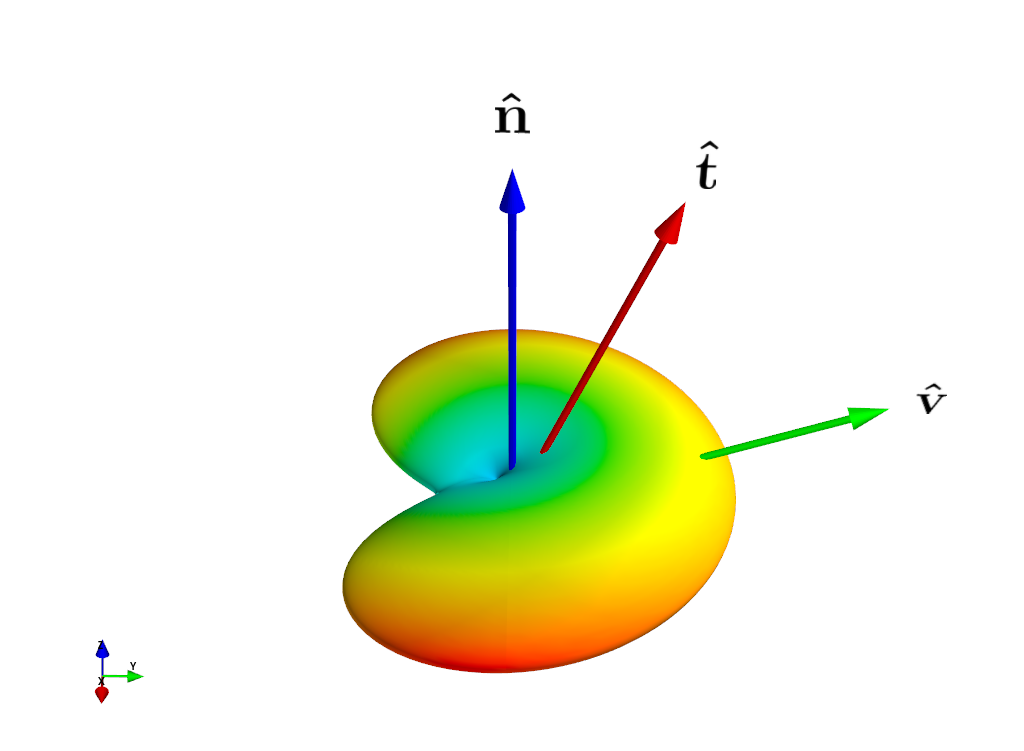
3D Plot:

Vary Schlick \(k\)

Vary Fiber (\(\mathbf{\hat{t}}\)) Polar Angle

Vary View (\(\mathbf{\hat{v}}\)) Polar Angle

Vary View (\(\mathbf{\hat{v}}\)) Azimuthal Angle

(Note: Normalized Amplitude)

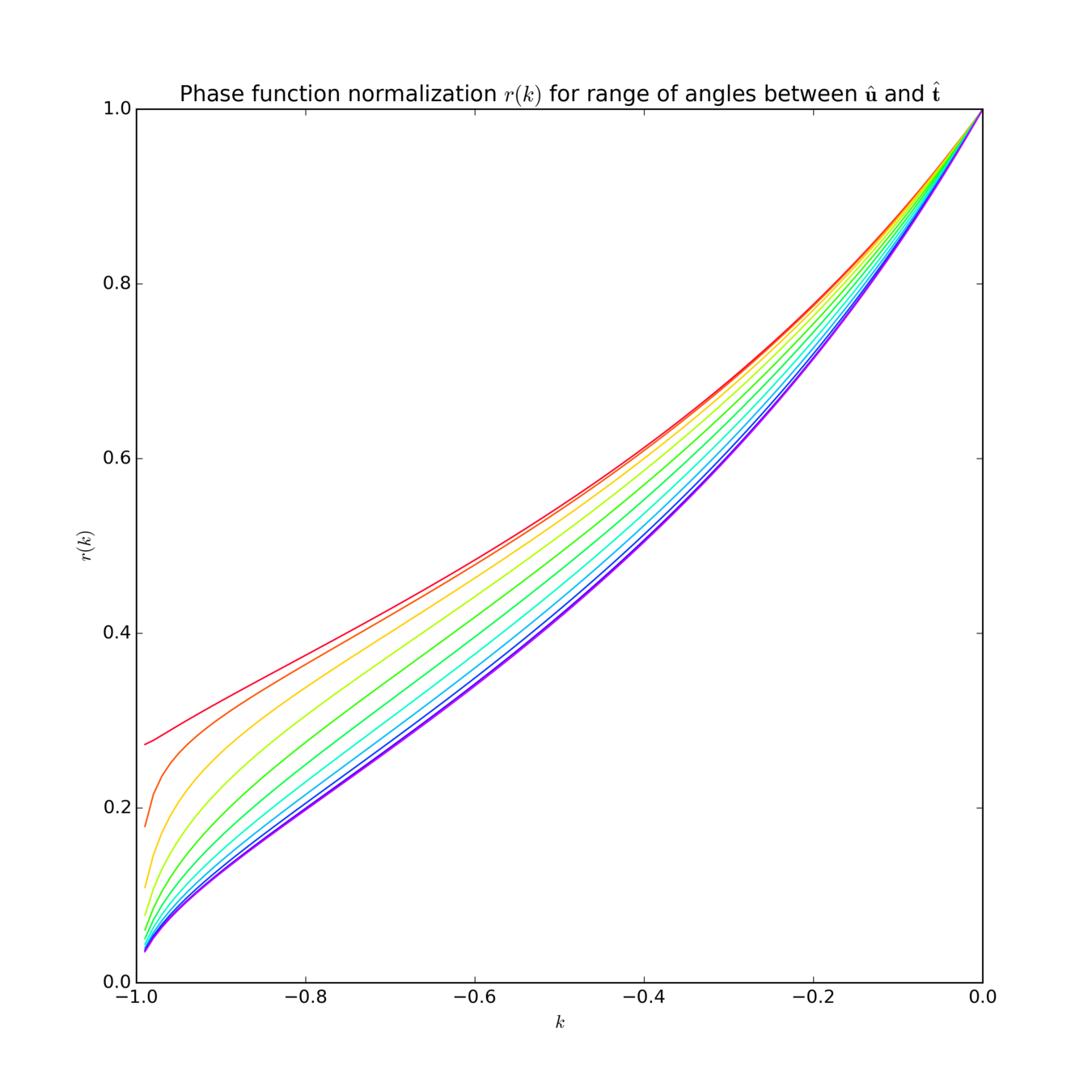
No analytical normalization term \(r(k)\) found for \(p_V\).
Fit a curve to \(r(k)\) with \(\mathbf{\hat{u}}\cdot\mathbf{\hat{t}}=0\), evaluated at shader compile time
- \(\mathbf{\hat{u}}\): Light direction
- \(\mathbf{\hat{t}}\): Fiber direction
- Ensures that energy is lost, not created
- Worst-case energy loss for sharp lobes when fiber direction and light direction aligned

Anisotropic Fuzz | Phase Function

More recent work: use a “fiber-like” specular SGGX phase function
- Analytical normalization

\(\mathbf{\hat{u}}\): Light direction
\(\mathbf{\hat{v}}\): View direction
\(\mathbf{\hat{h}}=\frac{\mathbf{\hat{u}}+\mathbf{\hat{v}}}{\left|\mathbf{\hat{u}}+\mathbf{\hat{v}}\right|}\): Half vector
\(\mathbf{\hat{t}}\): Fiber direction
\(\alpha\): GGX roughness
\(D_F\): (S)GGX “fiber” NDF
\(\sigma_F\): Microflake projected area
\(p_F(\mathbf{\hat{u}}, \mathbf{\hat{v}})\): Phase function

Anisotropic Fuzz | Phase Function

Using the SGGX phase function we get:

Anisotropic Fuzz | Phase Function

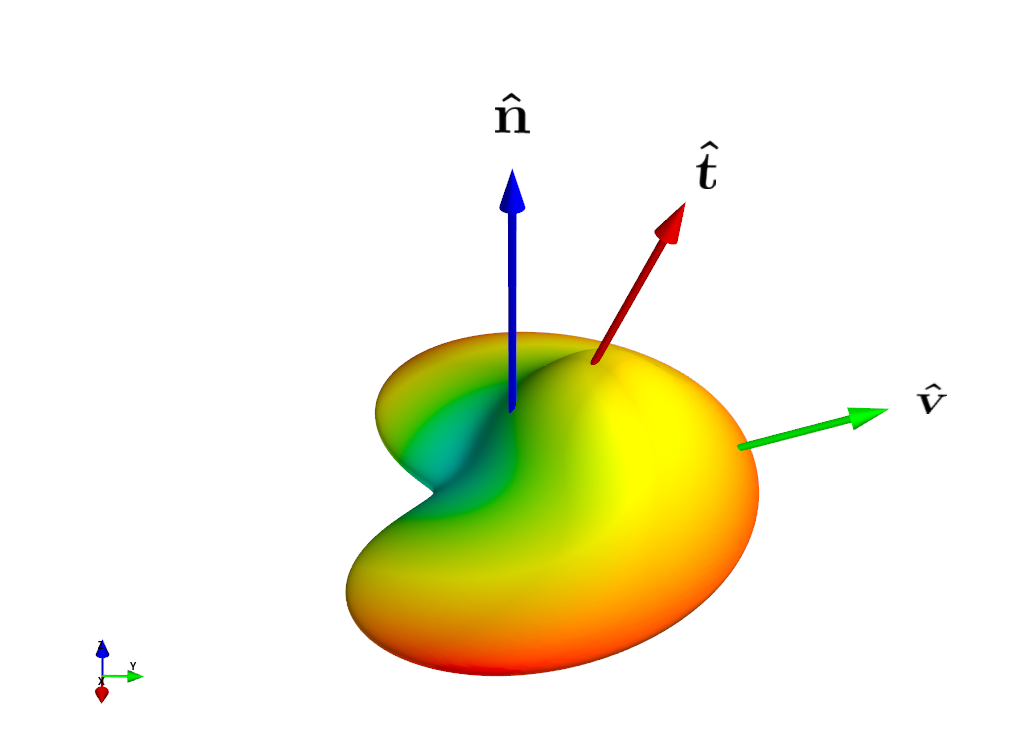
3D Plot:

Vary \(\alpha\)

Vary Fiber (\(\mathbf{\hat{t}}\)) Polar Angle

Vary View (\(\mathbf{\hat{v}}\)) Polar Angle

Vary View (\(\mathbf{\hat{v}}\)) Azimuthal Angle

(Note: Normalized Amplitude)

Anisotropic Fuzz | Shadowing

Need to account for shadowing of base layer by scattering layer
Don't account for all interactions to keep things simple(r)
Probability of a ray penetrating to the base layer without scattering is:

Probability of a ray reflected by the base layer escaping is:

Probability that an incident ray is scattered towards the base layer is:

Anisotropic Fuzz | Shadowing

Combining these, we get the following for the base layer attenuation:

No analytical expression for \(P_s\) (even for SGGX 😔)
Use the following approximation:

Anisotropic Fuzz | Ambient Lighting

Want anisotropy to continue to be visible in ambient lighting conditions
- For us this means spherical harmonic lighting + specular probes
Consider the rendering equation for our BRDF:

Anisotropic Fuzz | Ambient Lighting

Want anisotropy to continue to be visible in ambient lighting conditions
- For us this means spherical harmonic lighting + specular probes
Consider the rendering equation for our BRDF:

Approximate using:

Anisotropic Fuzz | Ambient Lighting

Now assume that \(L_i\) is approximately constant

Anisotropic Fuzz | Ambient Lighting

We've broken it down into:

Easy to compute from SH coefficients

Anisotropic Fuzz | Ambient Shadowing

Also need to account for ambient shadowing of base layer
Please see bonus slides

Anisotropic Fuzz | Ambient Shadowing

Also need to account for ambient shadowing of base layer
First consider diffuse ambient lighting only
Define:
- \(E_p\): Irradiance of the light penetrating the scattering layer
- \(E_s\): Irradiance of the light scattered down by the scattering layer
- \(\mathbf{c}_b\): Diffuse albedo of the base layer
- \(L_{b,o}\): Luminance of the base layer due to diffuse ambient lighting

Bonus Slide

Anisotropic Fuzz | Ambient Shadowing

Approximate using:
- Exact for uniform lighting

Bonus Slide

Anisotropic Fuzz | Ambient Shadowing

We've broken it down into:

\(\equiv E\), the irradiance on the surface (computed using SH)

Bonus Slide

Anisotropic Fuzz | Ambient Shadowing

Now for irradiance of light scattered onto base layer by scattering layer:

Approximate using:
- Exact for isotropic scattering and uniform lighting

Bonus Slide

Anisotropic Fuzz | Ambient Shadowing

We've broken it down into:

\(\equiv R(\theta_f, \alpha)\), constant for fixed \(\theta_f\) and \(\alpha\)

\(\equiv E\), the irradiance on the surface (computed using SH)

Bonus Slide

Anisotropic Fuzz | Ambient Shadowing

Putting it all together, we have

Bonus Slide

\newcommand{\Vector}[1]{\mathbf{#1}} \newcommand{\Color}[1]{\Vector{c}_{#1}} \newcommand{\Lum}[1]{L_{#1}} \newcommand{\Lb}[1]{L_{b,#1}} \newcommand{\Ld}[1]{L_{d,#1}} \newcommand{\Ls}[1]{L_{s,#1}} \newcommand{\Irr}[1]{E_{#1}} \newcommand{\diff}[1]{\, \text{d}#1} \newcommand{\zwsp}[0]{\hspace{0pt}} \newcommand{\V}[0]{\Vector{\hat{v}}} \newcommand{\U}[0]{\Vector{\hat{u}}} \renewcommand{\N}[0]{\Vector{\hat{n}}} \newcommand{\W}[0]{\Vector{\omega}} \newcommand{\T}[0]{\Vector{\hat{t}}} \newcommand{\h}[0]{\Vector{\hat{h}}} \renewcommand{\R}[0]{\Vector{\hat{r}}} \newcommand{\Ax}[1]{\widetilde{#1}} \begin{aligned} \Lb{o}(\V) &= \frac{\Color{b}}{\pi} P_e(\V) \left(E_p + E_s\right)\\ &\approx \frac{\Color{b}}{\pi} P_e(\V) \left[\Ax{Q} E + \Color{f} \left(1-\Ax{Q}\right) R E\right] \\ %&= \frac{\Color{b}}{\pi} P_e(\V) \operatorname{lerp}\left(\Color{f} R, 1, \Ax{Q}\right) E \\ &= \frac{\Color{b}\Color{\mathrm{atten}}}{\pi} E \\ \textrm{where} \\ \Color{\mathrm{atten}} &= P_e(\V) \left[\Ax{Q} + \Color{f} R \left(1-\Ax{Q}\right) \right] \\ %\Color{\mathrm{atten}} &= P_e(\V) \operatorname{lerp}\left(\Color{f} R, 1, \Ax{Q}\right) \end{aligned}

Anisotropic Fuzz | Ambient Shadowing

For specular ambient shadowing, we follow a similar approach
- Replacing SH sample with e.g. filtered reflection probe sample
- This lets us use the same \(\mathbf{c}_\mathrm{atten}\) attenuation term

Bonus Slide

For more common environmental materials (such as moss), we implemented a simplified version of this BRDF in our deferred shading
Please see bonus slides

Anisotropic Fuzz | Simplified Deferred Version

For more common environmental materials (such as moss), we implemented a simplified version of this BRDF for deferred shading
- 7-bit fuzziness value in G-Buffer (mapped to [0, 1])
Used a fixed set of parameters:
- \(\textrm{Density } d = 0.5\)
- \(\textrm{Spread} = 0.9\) (\(k_\mathrm{Schlick} \approx -0.1\), or \(\alpha_\mathrm{SGGX} \approx 0.95\))
- \(\mathbf{\hat{t}}_\mathrm{Fiber} = \mathbf{\hat{n}}_\mathrm{Vertex}\)
- \(\textrm{Fiber albedo } \mathbf{c}_\mathrm{Fiber} = 5 \cdot \mathbf{c}_\mathrm{Lambert}\)
For performance reasons, did not include base layer shadowing; instead we used:

Anisotropic Fuzz | Simplified Deferred Version

In the forward-shaded version, we expose a parameter to smooth normals (towards vertex normals) to give the scattering layer a softer appearance
Environment vertex normals were too inconsistent to use directly for shading
Instead we used wrap lighting to soften normals (McAuley 2013):

Anisotropic Fuzz | Simplified Deferred Version

Ghost didn't have any crushed velvet-like materials that made full use of the BRDF's capabilities
To demonstrate the technique, I created a “velvety” horse by modifying the Ghost horse shaders
Note that these results use the SGGX phase function, which is different than what shipped in Ghost
- In general, the results are qualitatively very similar
Disclaimer: Programmer art ahead!

Anisotropic Fuzz | Results

No Fuzz

Fuzziness Enabled With Parameters:

Density: 0.2
Spread: 0.2
Fiber Tilt: 23 degrees
Noisy Fiber Direction Map

No Base Layer Attenuation

Enabled Base Layer Attenuation
\(P_s(\mathbf{\hat{u}}) \equiv 0\)

\(P_s(\mathbf{\hat{u}})\) implemented

Vary Density \(d \;[0.0, 0.5]\)

Vary Spread \([0.0, 1.0]\)

Vary Fiber Tilt \(\theta_t \;[0.0, 90.0\degree]\)

Vary Fiber Color Saturation

Vary Fiber Color Value

Density: 0.1

Density: 0.2

Spread: 0.5

Spread: 1.0

Spread: 0.2

Fiber Tilt: 0 degrees

Fiber Tilt: 45 degrees

Fiber Tilt: 90 degrees

Fiber Tilt: 23 degrees

Fiber Color: Hot Pink

Deferred Fuzziness On

Deferred Fuzziness Off

Deferred Fuzziness On

Deferred Fuzziness Off

New anisotropic fuzz BRDF
- Able to reproduce the appearance of materials like crushed velvet
  - Under direct and indirect light
- Inexpensive enough to be used on PlayStation 4 hardware

Anisotropic Fuzz | Summary

Skin Shading

Using the Pre-Integrated Skin Shading technique (Penner and Borshukov, 2011)
Uses LUTs to compute subsurface scattering based on \(\mathbf{\hat{n}}\cdot\mathbf{\hat{l}}\) and curvature \(\kappa = \frac{1}{r}\)

\mathbf{\hat{n}}\cdot\mathbf{\hat{l}}

\frac{1}{r}

Skin Shading| Curvature

\theta

The LUT is computed by performing integration on a “ring”:

Skin Shading| Curvature

But it's better to think about it as being on a cylinder instead.
Two things to notice:
1. We want the curvature in the direction of the light
2. We need to take care about which scattering profile we're using

\theta

Skin Shading| Curvature

radial

linear

\theta

We want the directional curvature, not just the mean curvature
Can calculate directional curvature using the curvature tensor
- \(\mathbf{\hat{d}_i}\): Principal directions
- \(\kappa_i\): Principal curvatures
The curvature in direction \(\mathbf{\hat{l}}\) is found by

Skin Shading| Curvature

The curvature tensor \(\mathrm{I\!I}\) is a symmetric 2x2 matrix
Store \(\mathrm{I\!I}\) + mean curvature in 4-byte vertex channel
- Ambient lighting uses mean curvature
Calculate tangent-space curvature tensors as a pre-process
- Used algorithm described in Estimating Curvature and Their Derivatives on Triangle Meshes (Rusinkiewicz, 2004)
Blurred resulting curvature slightly
- Smooths out very high curvature at isolated vertices
- Used an equal blend of two Gaussians (\(\sigma_1= 0.8 \textrm{ cm}, \sigma_2 = 0.23 \textrm{ cm}\))
- Clamped concave curvature to zero for blur

Skin Shading| Curvature

Calculate \(\mathrm{I\!I}\) for each face using least squares with the following constraints:
Combine face \(\mathrm{I\!I}\) on vertices using “Voronoi area” weighting
- See paper for details

Skin Shading| Curvature

\newcommand{\Vector}[1]{\mathbf{#1}} \newcommand{\Color}[1]{\Vector{c}_{#1}} \newcommand{\Lum}[1]{L_{#1}} \newcommand{\Ld}[1]{L_{d,#1}} \newcommand{\Ls}[1]{L_{s,#1}} \newcommand{\Irr}[1]{E_{#1}} \newcommand{\diff}[1]{\, \text{d}#1} \newcommand{\zwsp}[0]{\hspace{0pt}} \newcommand{\V}[0]{\Vector{\hat{v}}} \newcommand{\U}[0]{\Vector{\hat{u}}} \renewcommand{\N}[0]{\Vector{\hat{n}}} \newcommand{\W}[0]{\Vector{\hat{\omega}}} \newcommand{\T}[0]{\Vector{\hat{t}}} \newcommand{\B}[0]{\Vector{\hat{b}}} \newcommand{\h}[0]{\Vector{\hat{h}}} \newcommand{\l}[0]{\Vector{\hat{l}}} \newcommand{\d}[0]{\Vector{\hat{d}}} \renewcommand{\S}[0]{\Vector{S}} \newcommand{\M}[0]{\Vector{M}} \newcommand{\Two}[0]{\mathrm{I\!I}} \newcommand{\e}[0]{\Vector{e}} \begin{aligned} \Two \begin{bmatrix} \e_0 \cdot \T \\ \e_0 \cdot \B \\ \end{bmatrix} &= \begin{bmatrix} \left(\N_2 - \N_1\right) \cdot \T \\ \left(\N_2 - \N_1\right) \cdot \B\\ \end{bmatrix} \\ \Two \begin{bmatrix} \e_1 \cdot \T \\ \e_1 \cdot \B \\ \end{bmatrix} &= \begin{bmatrix} \left(\N_0 - \N_2\right) \cdot \T \\ \left(\N_0 - \N_2\right) \cdot \B\\ \end{bmatrix} \\ \Two \begin{bmatrix} \e_2 \cdot \T \\ \e_2 \cdot \B \\ \end{bmatrix} &= \begin{bmatrix} \left(\N_1 - \N_0\right) \cdot \T \\ \left(\N_1 - \N_0\right) \cdot \B\\ \end{bmatrix} \end{aligned}

Comparison of:
- Zero curvature
- Mean curvature
- Directional curvature

Skin Shading| Results

Zero Curvature

Mean Curvature

Directional Curvature

Zero Curvature

Mean Curvature

Directional Curvature

Mean Curvature

Directional Curvature

Zero Curvature

Mean Curvature

Directional Curvature

No Curvature

Mean Curvature

Directional Curvature

No Curvature

Mean Curvature

Directional Curvature

Zero Curvature

Mean Curvature

Directional Curvature

Skin Shading| Implementation

float CurvatureFromLight(
    float3 tangent,
    float3 bitangent,
    float3 curvTensor,
    float3 lightDir)
{
    // Project light vector into tangent plane

    float2 lightDirProj = float2(dot(lightDir, tangent), dot(lightDir, bitangent));

    // NOTE (jasminp) We should normalize lightDirProj here in order to correctly
    //    calculate curvature in the light direction projected to the tangent plane.
    //    However, it makes no perceptible difference, since the skin LUT does not vary
    //    much with curvature when N.L is large.

    float curvature = curvTensor.x * GSquare(lightDirProj.x) +
                        2.0f * curvTensor.y * lightDirProj.x * lightDirProj.y +
                        curvTensor.z * GSquare(lightDirProj.y);

    return curvature;
}

New way of thinking about pre-integrated skin shading
- Use linear scattering profile/cylindrical integration for punctual light LUT generation
- Radial profile with spherical integration for SH lighting LUT
- Importance of directional curvature for improved accuracy

Skin Shading| Summary

Detail Maps

Bonus Slide

Detail Maps

Goals:
- Reduce texture memory usage by separating low- and high-frequency content
- Use library of tileable physically based materials for high frequency
- Intuitive authoring of low frequency (wear, grime, etc.)
- Combine in an efficient way at runtime
For normal maps, Reoriented Normal Mapping (Barré-Brisebois and Hill, 2012) works well
Want something that works well for other maps too
(albedo, specular, gloss, AO, etc.)

Bonus Slide

Traditionally, tiled detail maps are used to add high-frequency detail on top of low-frequency maps
- Using some kind of blending operator (overlay, additive, etc.)
No guarantee that the result makes sense
- Physically
- Matching desired appearance
- Needs interactive tuning
Unclear how to generate from scanned materials
- Usually needs preprocessing
Combining two compressed textures
- Potential for increased artifacts

Detail Maps| Traditional Approach

Bonus Slide

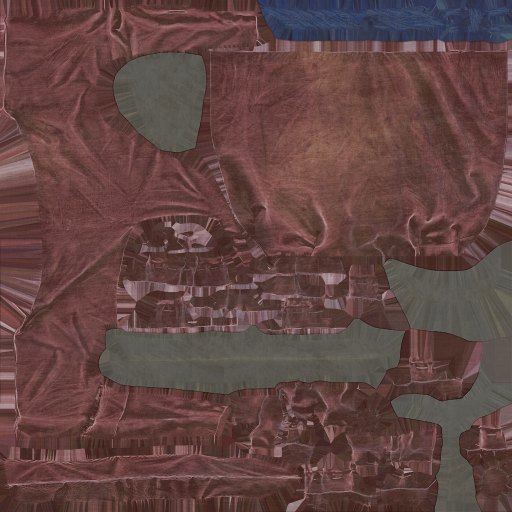
Start with tiled materials and paint low-frequency content on top
Synthesize a map such that:

Detail Maps| Our Approach

\textrm{Synthesized Map} \otimes \textrm{Tiled Detail Layers} = \textrm{Target Map}

s \otimes d = t

\otimes

Bonus Slide

Use Substance Designer and Substance Painter for authoring
- Added SD nodes that match our shader UV and HSV transforms
Set up tiled materials (up to 3 combined with masks)
Paint on top to generate a target map
- This is what artists export for use in our shaders
At asset compile time:
- Process target + tiled layers and masks
- Generate a new synthesized map

Detail Maps| Workflow

Bonus Slide

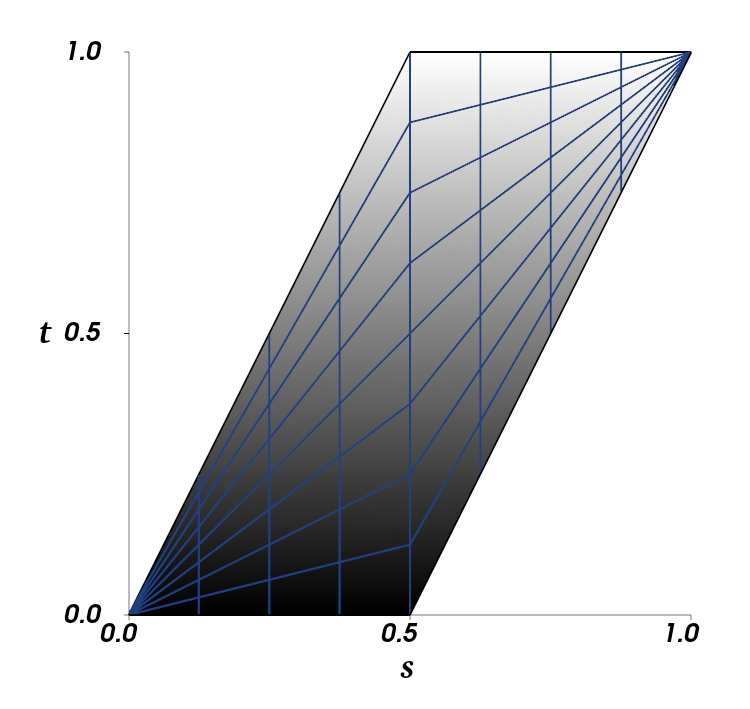
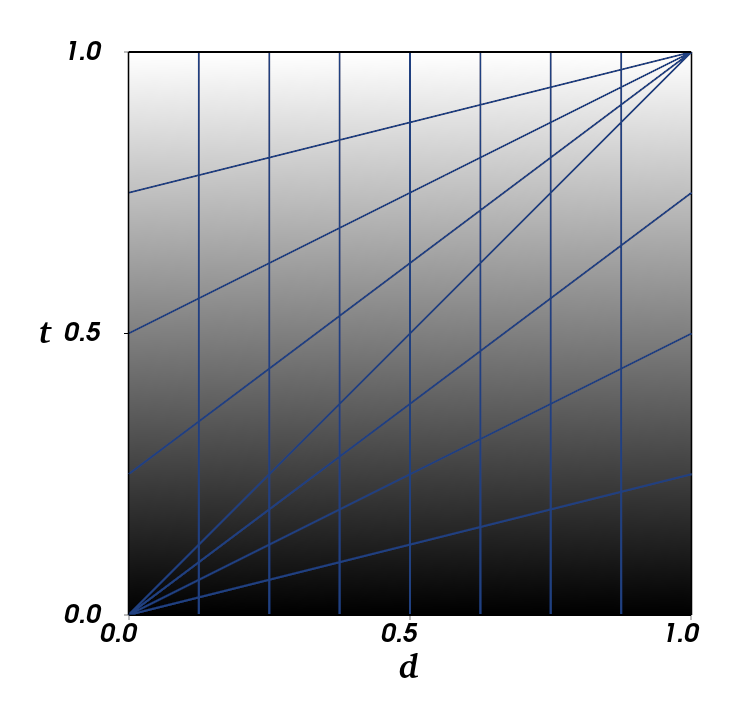
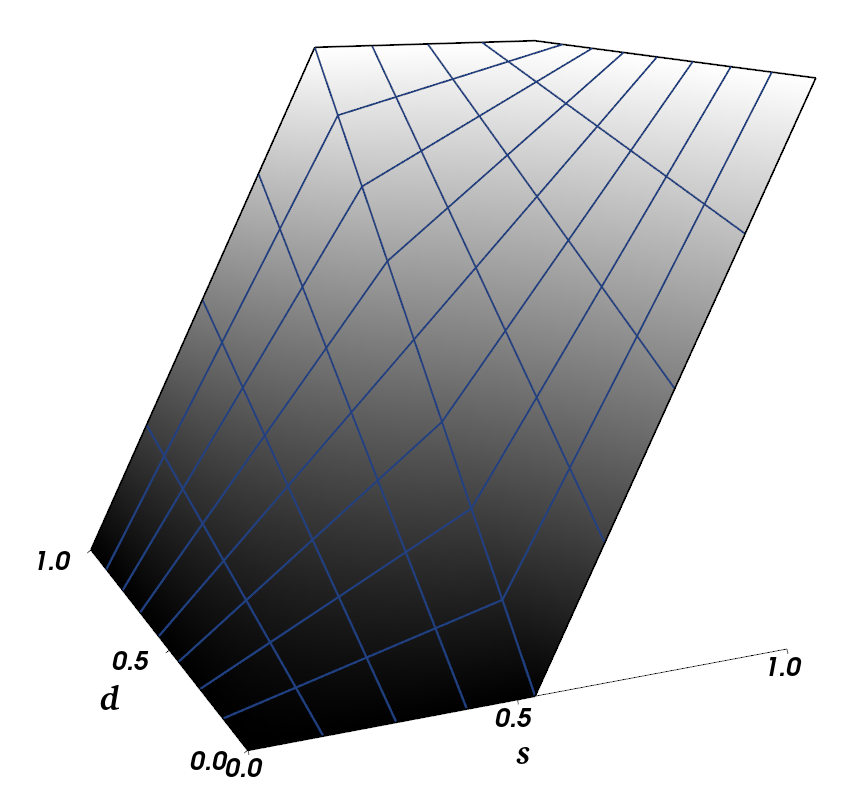
What blend operator \(\otimes\) should we use?
Need to ensure that a solution exists for \(s\) in
- \(s\): Synthesized map
- \(d\): Detail map
- \(t\): Authored target map
Excludes hard light, soft light, screen, multiply, etc.
Overlay works fairly well:

Detail Maps| Blending

s \otimes d = t \quad \forall d, t \in \left[0, 1\right]

f_{overlay}(s, d) = \left\{\begin{matrix} 2sd, & s < 0.5 \\ 1-2\left(1-s\right)\left(1-d\right), & s \ge 0.5 \end{matrix}\right.

Bonus Slide

Detail Maps| Blending

f_{overlay}(s, d) = \left\{\begin{matrix} 2sd, & s < 0.5 \\ 1-2\left(1-s\right)\left(1-d\right), & s \ge 0.5 \end{matrix}\right.

\otimes

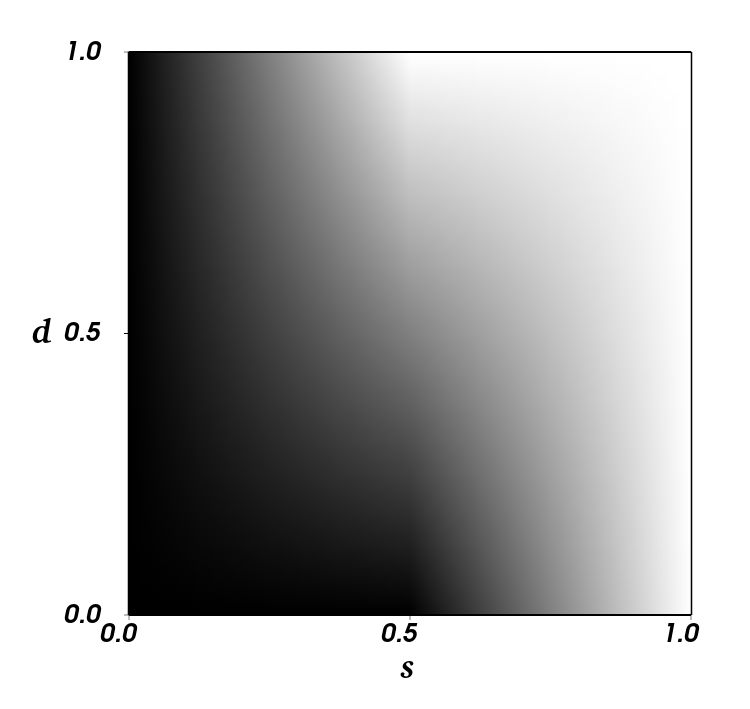
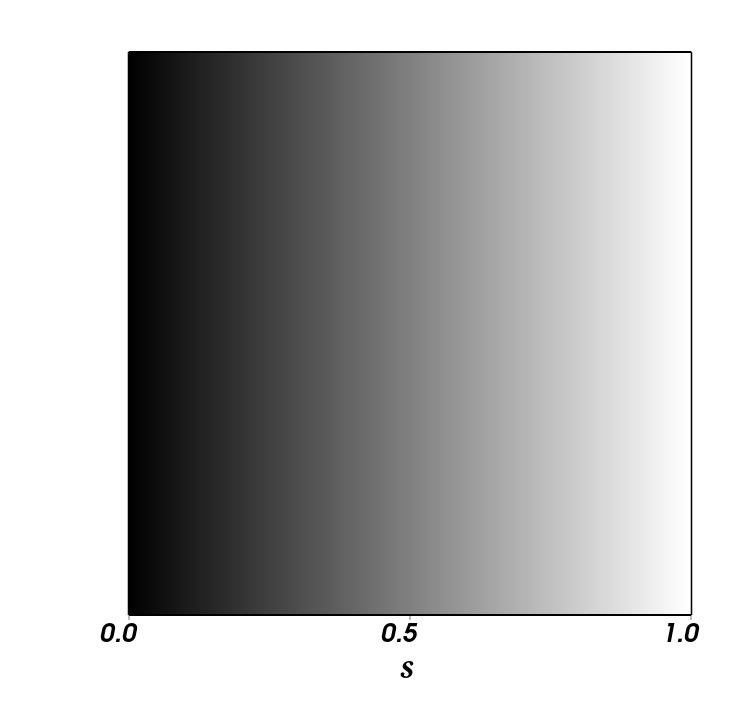
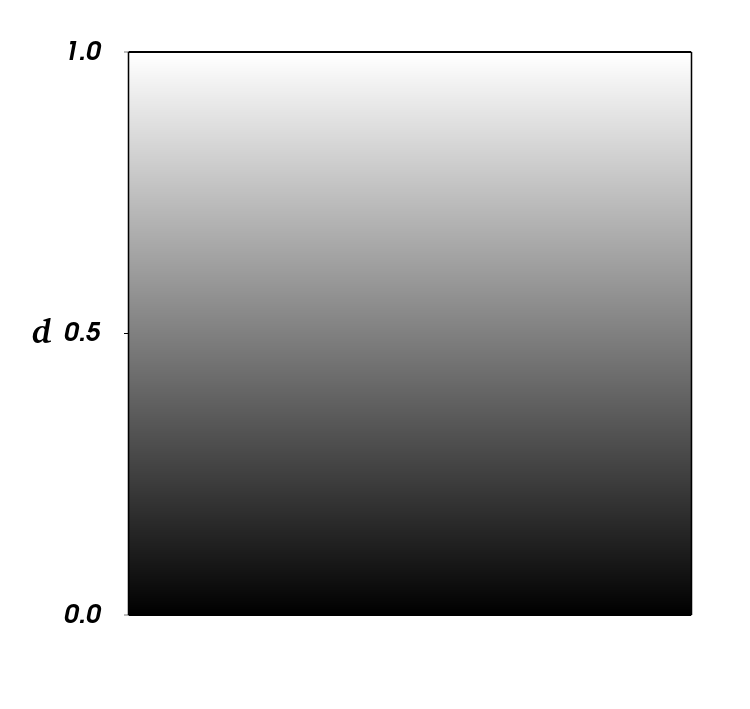
Synthesized

Detail

Target

Bonus Slide

Detail Maps| Blending

f_{overlay}(s, d) = \left\{\begin{matrix} 2sd, & s < 0.5 \\ 1-2\left(1-s\right)\left(1-d\right), & s \ge 0.5 \end{matrix}\right.

d=0

d=1

s=0.875

s=0.125

Bonus Slide

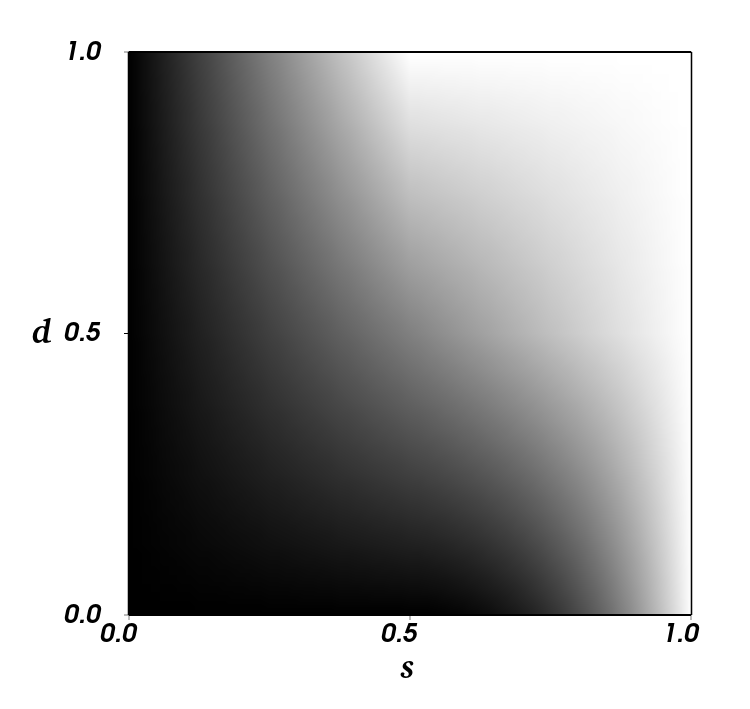
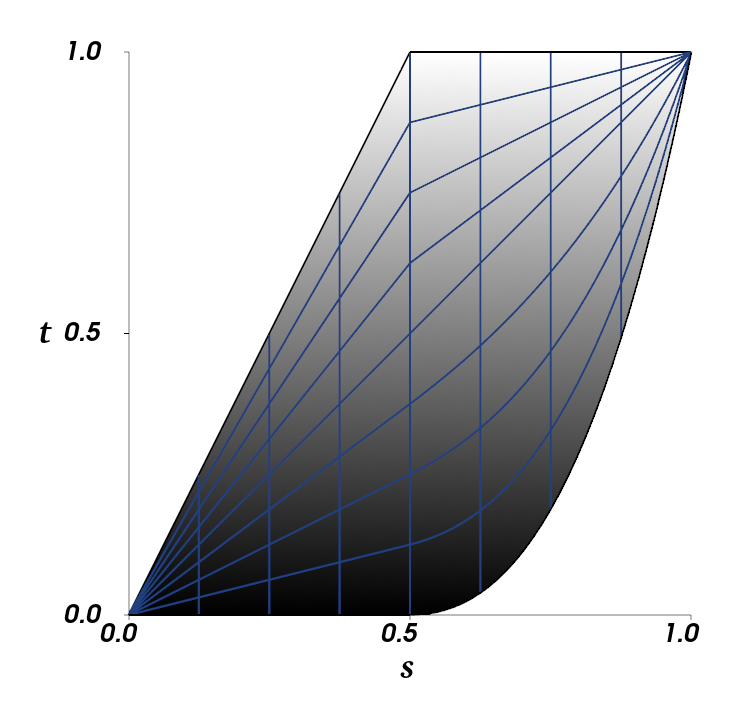
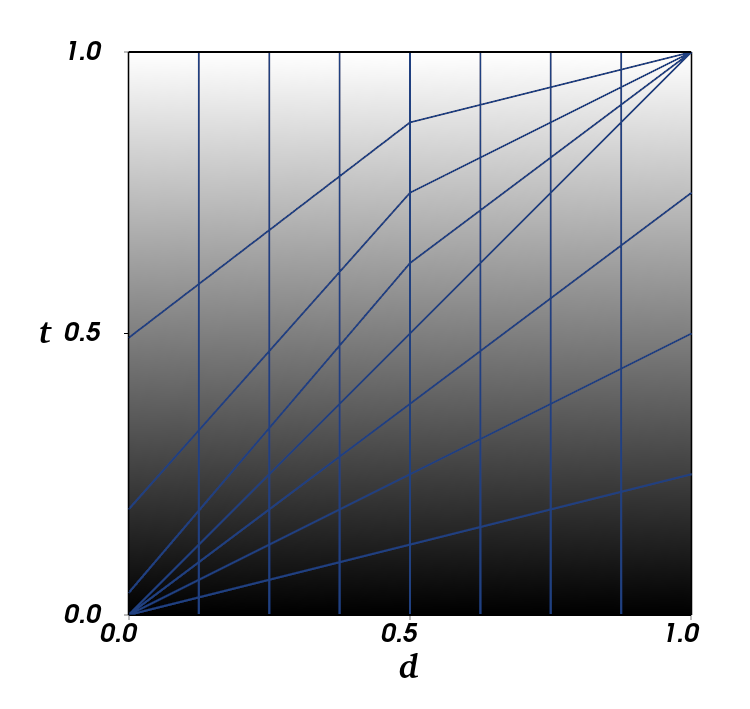
Precision gets worse as detail \(d\) approaches 0 and 1
- Relative precision especially bad as \(d\) approaches 0
Noticeable quality degradation when using BC1
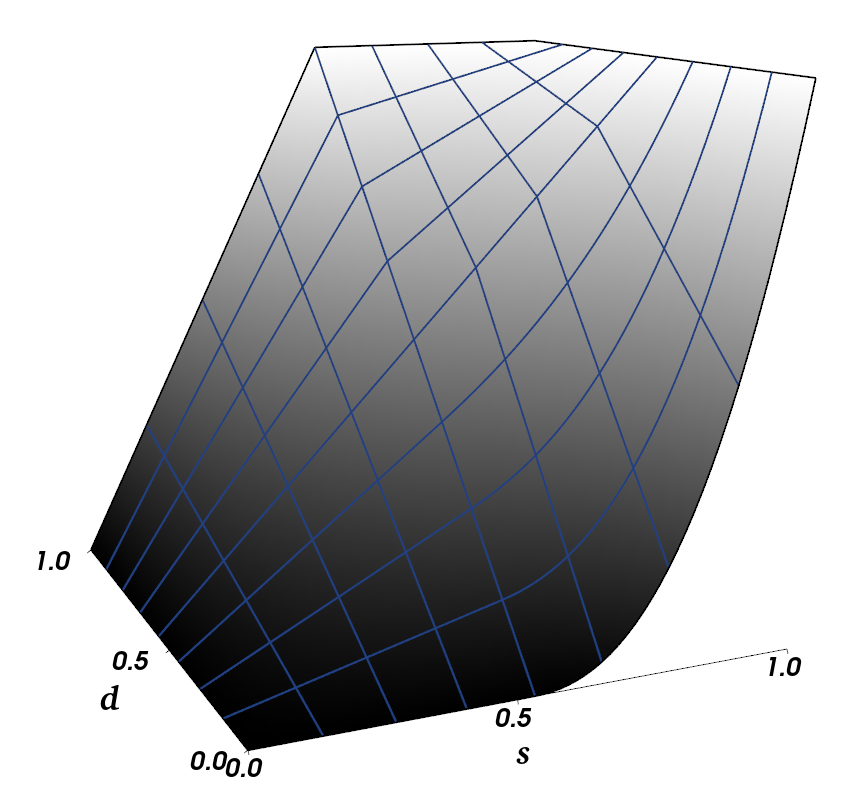
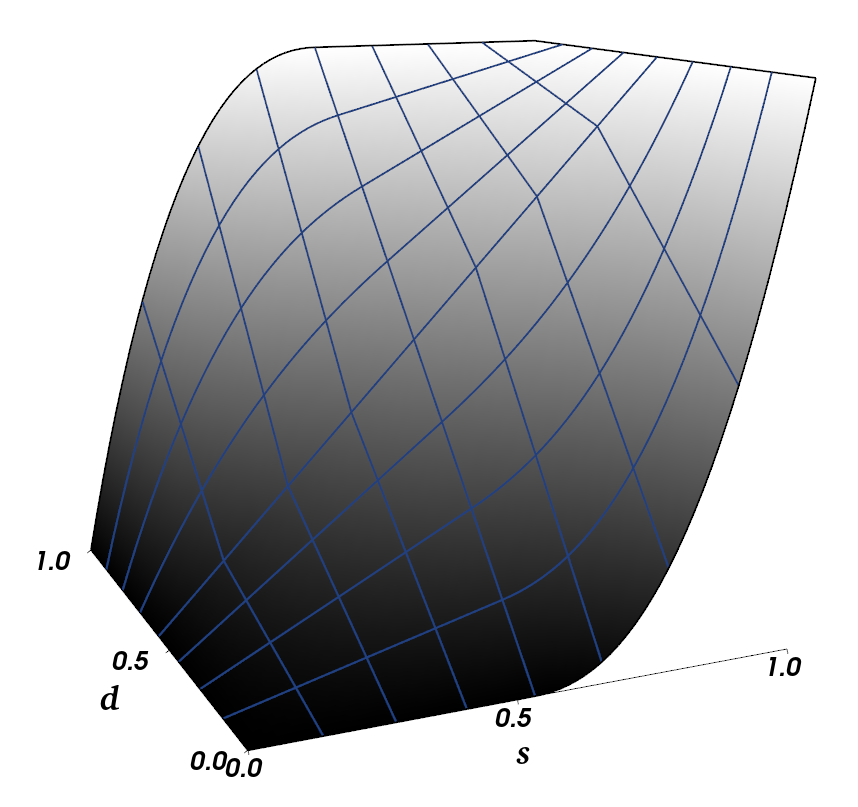
Wanted to increase precision when target \(t\) is near \(d\)
- Especially when brightening dark tiled layers
- Led us to modify the blending equation:

Detail Maps| Precision

f_{os}(s, d) = \left\{\begin{matrix} 2sd, & s < 0.5 \\ 1-2\left(1-s\right)\left(1-d\right), & s \ge 0.5 \textrm{ and } d \ge 0.5 \\ \operatorname{lerp}\left(2sd, s, \left(2s -1\right)^2\right), &s \ge 0.5 \textrm{ and } d \lt 0.5 \end{matrix}\right.

Bonus Slide

Detail Maps| Precision

Bonus Slide

Detail Maps| Precision

f_{oss}(s, d) = \left\{\begin{matrix} 2sd, & s < 0.5 \textrm{ and } d < 0.5 \\ 1-2\left(1-s\right)\left(1-d\right), & s \ge 0.5 \textrm{ and } d \ge 0.5 \\ \operatorname{lerp}\left(2sd, s, \left(2s -1\right)^2\right), &s \ge 0.5 \textrm{ and } d \lt 0.5 \\ \operatorname{lerp}\left(1-2\left(1-s\right)\left(1-d\right), s, \left(2s -1\right)^2\right), &s \lt 0.5 \textrm{ and } d \ge 0.5 \end{matrix}\right.

Detail Maps| Precision

f_{overlay}(s, d) = \left\{\begin{matrix} 2sd, & s < 0.5 \\ 1-2\left(1-s\right)\left(1-d\right), & s \ge 0.5 \end{matrix}\right.

Bonus Slide

Detail Maps| Precision

Bonus Slide

Detail Maps| Precision

Bonus Slide

Detail Maps| Precision

No Detail

Bonus Slide

Detail Maps| Precision

Only Detail

Bonus Slide

Detail Maps| Precision

\otimes

Synthesized

Detail

Target

Bonus Slide

Detail Maps| Precision

Target

Bonus Slide

Detail Maps| Precision

Target BC1

RMSE: 1.95

Bonus Slide

Detail Maps| Precision

Standard Overlay Blend

RMSE: 1.74

Bonus Slide

Detail Maps| Precision

Smooth Overlay Blend (Ours)

RMSE: 1.60

Bonus Slide

Detail Maps| Precision

Target BC1 Error

RMSE: 1.95

Bonus Slide

Detail Maps| Precision

Standard Overlay Blend Error

RMSE: 1.74

Bonus Slide

Detail Maps| Precision

Smooth Overlay Blend Error (Ours)

RMSE: 1.60

Bonus Slide

Blending two sets of compressed textures
- Exacerbates compression artifacts
Reduce by synthesizing texture against compressed tiled maps
- Except for top mip which is magnified against multiple detail mips

Detail Maps| Compression

Bonus Slide

Target

Detail Maps| Compression

Bonus Slide

Blend without Compression Compensation

Detail Maps| Compression

RMSE: 1.70

Bonus Slide

Blend with Compression Compensation (Ours)

Detail Maps| Compression

RMSE: 1.60

Bonus Slide

Error without Compression Compensation

Detail Maps| Compression

RMSE: 1.70

Bonus Slide

Error with Compression Compensation (Ours)

Detail Maps| Compression

RMSE: 1.60

Bonus Slide

Detail Maps| Compression

Bonus Slide

Detail Maps| Compression

Bonus Slide

Detail Maps| Compression

No Detail

Bonus Slide

Detail Maps| Compression

Only Detail

Bonus Slide

\otimes

Synthesized

Detail

Target

Detail Maps| Compression

Bonus Slide

Target

Detail Maps| Compression

Bonus Slide

Blend without Compression Compensation

Detail Maps| Compression

RMSE: 2.43

Bonus Slide

Blend with Compression Compensation (Ours)

Detail Maps| Compression

RMSE: 2.00

Bonus Slide

Target

Detail Maps| Compression

Error without Compression Compensation

Detail Maps| Compression

RMSE: 2.43

Bonus Slide

Error with Compression Compensation (Ours)

Detail Maps| Compression

RMSE: 2.00

Bonus Slide

\otimes

Synthesized

Detail

Target

Detail Maps| Compression

Target

Detail Maps| Compression

Blend without Compression Compensation

Detail Maps| Compression

PSNR: 39.53

Blend with Compression Compensation (Ours)

Detail Maps| Compression

PSNR: 43.55

Analyzed second mipmap of 1743 material color textures in game
Average compressed target RMSE: 5.67
Average detail-blended RMSE: 5.81
- 0.14 (2.5%) higher than with no detail
Average RMSE using standard overlay blend: 5.89
- 0.09 (1.5%) higher than ours (\(\Delta\)RMSE 61% higher)
Average RMSE without compression compensation: 5.87
- 0.06 (1.1%) higher than ours (\(\Delta\)RMSE 44% higher)
- Recall that first mipmap doesn't use compression compensation

Detail Maps| Statistics

Bonus Slide

Normal maps blended using Reoriented Normal Mapping (Barré-Brisebois and Hill, 2012)
- https://blog.selfshadow.com/publications/blending-in-detail/
- Compute like other maps (by inverting the blend function)
Anisotropic specular (“aniso”) maps blended with regular alpha blending
- I.e., “over” operator
- Alpha is a shader parameter

Detail Maps| Other Blend Modes

Bonus Slide

Detail Maps | Summary

Successful widespread adoption of detail maps for Ghost
Advantages over traditional approach:
- Can selectively cancel out lower frequency components of detail
- More potential texture reuse since detail can be used as material
Disadvantages:
- Slightly longer texture processing
- Slightly higher RMSE on average for color textures (vs no detail)
  - Can be reduced by centering histogram of detail maps
    - I.e., same type of preprocessing used with traditional detail maps

Bonus Slide

Acknowledgements

My wife and son for their patience while I went from finishing Ghost to working on this presentation
Sucker Punch rendering programmers:
- Adrian Bentley
- Bill Rockenbeck
- Eric Wohllaib (who implemented deferred fuzziness)
- Matthew Pohlmann
- Tom Low
Drew Harrison, Harold Lamb, Joanna Wang, Omar Aweidah, and Phillip Jenne for their assistance with assets for this talk
Everybody at Sucker Punch for making everything awesome
Steve McAuley and Stephen Hill for the insightful feedback

References

[DHI+13] Jonathan Dupuy, Eric Heitz, Jean-Claude Iehl, Pierre Poulin, Fabrice Neyret, and Victor Ostromoukhov. Linear efficient antialiased displacement and reflectance mapping. ACM Trans. Graph., 32(6), November 2013.

[HDCD15] Eric Heitz, Jonathan Dupuy, Cyril Crassin, and Carsten Dachsbacher. The SGGX microflake distribution. ACM Trans. Graph., 34(4), July 2015.

[KK89] J. T. Kajiya and T. L. Kay. Rendering fur with three dimensional textures. SIGGRAPH Comput. Graph., 23(3):271–280, July 1989.

[KP03] Jan Koenderink and Sylvia Pont. The secret of velvety skin. Machine Vision and Applications, 14(4):260–268, 2003.

[McA13] Steve McAuley. Extension to energy-conserving wrapped diffuse. http://blog.stevemcauley.com/2013/01/30/extension-to-energy-conserving-wrapped-diffuse/, January 2013.

[MHH+12] Stephen McAuley, Stephen Hill, Naty Hoffman, Yoshiharu Gotanda, Brian Smits, Brent Burley, and Adam Martinez. Practical physically-based shading in film and game production. In ACM SIGGRAPH 2012 Courses, SIGGRAPH ’12, New York, NY, USA, 2012. Association for Computing Machinery.

[OB10] Marc Olano and Dan Baker. Lean mapping. In Proceedings of the 2010 ACM SIGGRAPH Symposium on Interactive 3D Graphics and Games, I3D ’10, page 181–188, New York, NY, USA, 2010. Association for Computing Machinery.

[PB11] Eric Penner and George Borshukov. Pre-integrated skin shading. In Wolfgang Engel, editor, GPU Pro 2, chapter 1. A K Peters/CRC Press, New York, 1st edition, 2011.

[PH10] Matt Pharr and Greg Humphreys. Physically Based Rendering, Second Edition: From Theory To Implementation, pages 583–587. Morgan Kaufmann Publishers Inc., San Francisco, CA, USA, 2nd edition, 2010.

[RH01a] Ravi Ramamoorthi and Pat Hanrahan. An efficient representation for irradiance environment maps. In Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH ’01, pages 497–500, New York, NY, USA, 2001. ACM.

[RH01b] Ravi Ramamoorthi and Pat Hanrahan. On the relationship between Radiance and Irradiance: Determining the illumination from images of a convex Lambertian object. Journal of the Optical Society of America, 18(10):2448–2459, Oct 2001.

[Rus04] Szymon Rusinkiewicz. Estimating curvatures and their derivatives on triangle meshes. In Symposium on 3D Data Processing, Visualization, and Transmission, September 2004.

[RV11] P. Ramachandran and G. Varoquaux. Mayavi: 3D Visualization of Scientific Data. Computing in Science & Engineering, 13(2):40–51, 2011.

Text