Spectral Rendering in a Non-Spectral Renderer: How Can we Author and Render Fluorescence in RGB?

Spectral Rendering in a Non-Spectral Renderer:
How Can we Author and Render Fluorescence in RGB?

Laurent Belcour

Alban Fichet

Pascal Barla

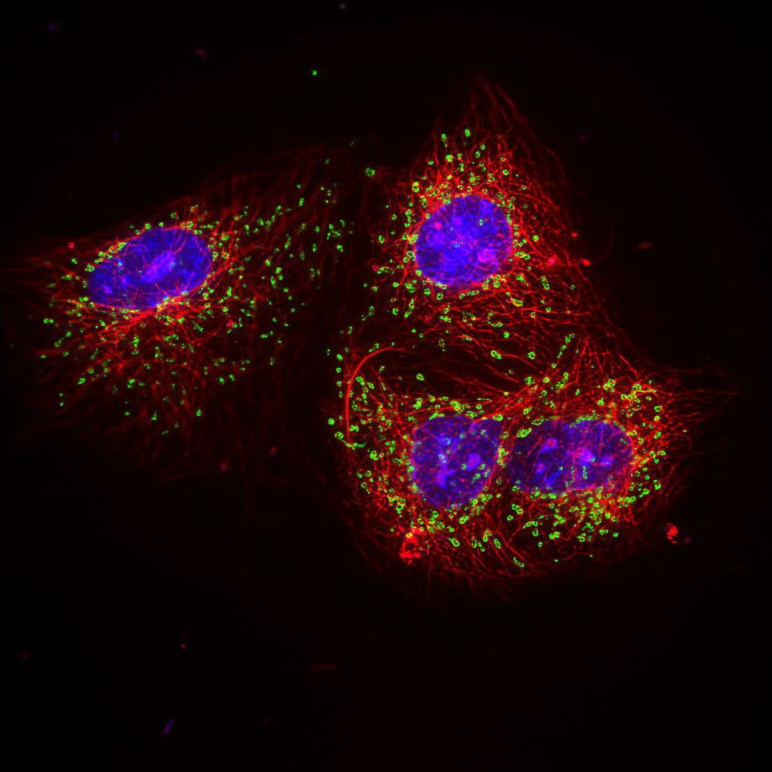
More Fluorescence

A Fluorescent Material Model for Non-Spectral Editing & Rendering

Thursday 9am - 10:30am
West Building, Rooms 301-305

Fluorescence

Under daylight - image from Reveal Nature

https://www.photonews.ca/exploring-fluorescent-nature/

Under spot light - image from Don Komarechka

https://nightsea.com/nature/minerals/sodalite-fluorescence/

Under white light - image from nightsea.com

https://www.leica-microsystems.com/science-lab/life-science/multicolor-microscopy-the-importance-of-multiplexing/

All bands - image from Leica Microsystems

image from Tough Duck

But what is fluorescence? *click* To understand it, let's see fluorescence in action. For example this hedgehog under daylight. *click*

Now, if we illuminate the same object with an ultra-violet light – light that is invisible to the human eye – we can still see it. This is one very interesting aspect of fluorescence. This behavior cannot be modeled using what we use classically in rendering. *click*

Interestingly, a lot of species are fluorescent. For example, this flower might not look fluorescent to us. *click*. But its petals are. *click*

We also find fluorescence in minerals. For example this sodalite rock. Under white light it looks like a regular rock. *click*. But under UV light, the different constituents of the rock are highlighted by separate re-radiated colors. *click*

Fluorescence is widely used in scientific imaging. In this image, different parts of a biological organ are highlighted by injecting fluorescent proteins that interact with specific elements of the organ. *click*. Using color segmentation, we can highlight specific structures of an organ. *click*

We also design objects using fluorescence. For example, those safety jackets use both retro-reflectivity and fluorescence to improve the visiblity of people. *click*

Physics of Fluorescence

Absorption and re-emission of light by atoms/molecules
- See Molecular Fluorescence by Valeur and Berberan-Santos

Now how does fluorescence work? For our purpose, we are going to approximately characterize fluorescence as the instantaneous absorption and re-emission of light by matter in which the light's frequency is changed. *click*

For a precise description of fluorescence at the molecular level, the book of Valeur and Berberan-Santos is a good read. But how can light be re-emitted at a different frequency? *click*

Here is formaldehyde, a simple molecule composed of carbon, hydrogen and oxygen. *click*. The molecular binding between the carbon and oxygen can take have different "energy levels" depending on its geometrical configuration. *click*. When light is absorbed by this binding, the electronic configuration can change state *click* using the energy of the absorbed photon. Later, the molecule can change to a different energy configuration (here S1). This change of energy is associated with the release of a photon. If the energy difference is not the same as during absorption, the emitted light will have a different frequency. *click*.

Physics of Fluorescence

A common description: the re-radiation matrix

$$ \mathcal{R}(\lambda_i, \lambda_o) = $$

$\lambda_i$

$\lambda_o$

Physically based Fluorescence

Re-radiation has two components
- Diagonal: traditional albedo
- Off-Diagonal: fluorescence

Cannot re-radiate at smaller wavelengths
- Photon energy inversely proportional to wavelength

Energy conservation

$$ \mathcal{R} = $$

Cannot re-radiation $\Delta E > S_2-S_0$ $\rightarrow {\color{orange}\lambda_o} \geq {\color{purple}\lambda_i}$

$$\int \mathcal{R}(\lambda_i, \lambda_o) \mbox{d}\lambda_o \leq 1$$

$$\lambda_i$$

The re-radiation matrix has a structure derived from the physical process of fluorescence. *click*

First, it has two components: *click*

A diagonal component: this is what we are used to calling the albedo. This is the part of the re-radiation matrix where the wavelength of re-emission equals the wavelength of absorbed light. *click*
The Off-Diagonal component: everything else is what we are used to calling the fluorescence. *click*

Second, there are also constraints on the re-radiation matrix. The most important one seems to be, that for a single photon absorption, re-emitted light is only at higher wavelengths. That is above the diagonal. *click*. This is due to what we saw previously in the Jablonski diagram: when a photon is absorbed, the molecule cannot re-emit a photon with a higher energy level. *click*. Since energy is inversely proportional to the wavelength, it means it can only re-emit at higher wavelengths. *click*

The third and important element is energy conservation. For a given incoming wavelength, we cannot re-emit more light than we absorb. *click*

Spectral Rendering with Fluorescence

Requires an additional sampling step
- See [Mojzik et al. 2018] for details
- Create a conditional CDF from data / model


					Spectrum Li(Ray ray, Sampler sampler)
					{
						/* Intersect scene with ray and obtain surface BSDF */
						BSDF bsdf;

						/* Only highlighting BSDF sampling strategy */
						[...]
						
						// Sample the outgoing direction
						ray.wo = bsdf.sample(ray.wo, sampler);

						// Sample the outgoing wavelength
						// Consumes one random number
						ray.wavelength = bsdf.rerad.sample(ray.wavelength, sampler);

						return Li(ray, sampler)
					}

[Mojzik et al. 2018]

The re-radiation matrix is the formalism that makes fluorescence directly pluggable into spectral renderers. If one wants to add fluorescence to a stochastic spectral renderer, the required change is "simply" an additional sampling step during path tracing. *click*

Ok, it is not quite as easy as that, but not far off. I refer you to the work of Mojzik and colleagues for the nitty-gritty of it. *click*

Here is a snippet of a surface interaction in a path tracer highlighting the BSDF sampling strategy. *click*. If we want to integrate fluorescence, we have to change the wavelength of the outgoing ray before tracing it. *click*. For that we use the re-radiation matrix. *click* For the incident ray's wavelength, we importance sample the slice of the re-radiation matrix. *click* To do so, we need to invert the CDF of the slice. This is easy to do since it resembles environment map sampling. *click*

RGB Rendering with Fluorescence

RGB Rendering is a form of spectral Rendering
- See [Fichet el al. 2024]

reduced matrix

light source

material

color matching functions

But how do you incorporate fluorescence into an RGB renderer, where sampling new wavelengths doesn't make sense? From that perspective alone, it appears that fluorescence requires a spectral renderer. *click*

With my colleagues Alban Fichet and Pascal Barla, we found that if you express RGB rendering as a special form of spectral rendering, fluorescence becomes achievable. *click*

For that we will take the example of this material directly lit by a point light using a spectral renderer. *click*. When we illuminate a fluorescent object with a light, we take the light's spectrum as a dense vector and *click* multiply it with the re-radiation matrix. This gives us a reflected spectrum that *click* we must integrate with the spectral sensitivity of the camera (here I took CIE XYZ 2006). The output is an RGB triplet that we can splat into a pixel. *click*

To express this as RGB (or XYZ) rendering, we first have to downscale the spectral light source to an RGB (or XYZ) triplet. This triplet is what we are going to propagate during ray tracing. *click*. At surface interaction, we have to upscale the color triplet to a spectra. This spectra can now be used as input to the re-radiation matrix to get the outgoing spectra. *click*. We need to downscale this spectra to RGB to carry on tracing. *click*. At camera, we can use the transfer matrix to the camera color space to get the sample's color.

Now this is only a theoretical view of what would happen. *click* In practice you would like to avoid the upscaling and downscaling parts during material evaluation. *click*. We found that this is possible for fluorescence, and the re-radiation matrix can be replaced by a reduced matrix working on color triplets. *click*

Spectral Reduction of Fluorescence

Analytic if up and down are linear operators
- We can use the XYZ CMFs ${\color{green} s_i}$ and their duals ${\color{blue}\tilde s_i}$ as a basis

Baked prior to rendering
- For measured data, simple a two matrix products

$$ F_{kl} = \iint {\color{green} s_k(\lambda_o)} \; \mathcal{F}(\lambda_i, \lambda_o) \; {\color{blue} \tilde{s}_l(\lambda_o)} \; \mbox{d}\lambda_i \, \, \mbox{d} \, \lambda_o $$


								def ReduceRerad(R: np.array):
									S  = CMF('XYZ_CIE_2006.csv')      													# (N,3)
									Sb = np.linalg.pinv(S @ S.T) @ S  													# (N,3)
									
									r = S.T @ R @ Sb                  													# (3,3)
									return r

What we showed in our EGSR paper last year is that if we use linear operators for upscale and downscale, this reduction matrix can be computed. *click*

A very simple linear downscale is to use the dot product with the color matching functions. Integrating a spectra with the XYZ CMFs output the XYZ triplet of that spectrum. It turns out that the dual basis of the CMF is a way to upscale a triplet to a spectra. *click*

Here is how the reduced matrix is computed. *click*

The different values of the reduced matrix are defined as the double integral *click* of the downscale basis (here the XYZ CMFs) *click* multiplied by the re-radiation function *click* times the upscale basis (here the dual of the XYZ CMFs).

In practice, for measured data, both the CMFs, their duals, and the re-radiation are tabulated and integration would be done using matrix multiplications. Typical Python code for computing the reduced matrix would look like this. *click* Taking as input a dense re-radiation, *click* as well as the CMFs used during light transport. *click* The dual basis can be computed on the fly and it uses a pseudoinverse for numerical stability. *click* Finally, two matrix multiplications are used to evaluate the reduced matrix at once. *click*

Spectral Reduction of Fluorescence

Analytic if up and down are linear operators
- We can use the XYZ CMFs $s_i$ and its dual $\tilde s_i$ as a basis

Baked prior to rendering
- For measured data, simple a two matrix products
- Parametric models are better with analytical integration

[Belcour et al. 2025]

Spectral Reduction: Example on Measured Data

First: Upscale data to the CMFs density
- Scaling must preserve energy!
- Different interpolation weights between $\lambda_i$ and $\lambda_o$

HERPICER

10 nm per band

Interpolated data

1 nm per band

Reduced matrix $R$

Spectral Reduction: Example on Measured Data

First: Upscale data to the CMFs density
- Scaling must preserve energy!
- Different upscale between $\lambda_i$ and $\lambda_o$

Second: direct illumination computation
- Multiply matrix with light triplet: $\mathbf{c} = R \times \mathbf{l}$


						Color DirectLi(Ray ray, Sampler sampler)
						{
							/* Intersect scene with ray and obtain surface BSDF */
							BSDF bsdf;

							/* Direct illumination only samples the light */
							Color l = sample_light(ray.wo, ray.p, sampler);

							/* Matrix multiplication using HLSL syntax */
							Color li = mul(bsdf.rerad, l);
							return li;
						}

RGB Rendering - Reduced

Spectral Rendering

Spectral Reduction: Basis

Using more than three channels for UVs

350nm emission

RGB Rendering - Reduced

Spectral Rendering

RGBU Rendering - Reduced with UV

no overlap

I would like to stress that the accuracy of the reduced matrix compared to the spectral reference is largely due to the basis used for the downscale operator. *click*

Let me illustrate this using a very crude example where we illuminate a fluorescent object with an invisible light (here monochromatic at 350 nm). We can see that this material re-emits a greenish spectrum. *click* But if we reduce the associated re-radiation matrix with the traditional XYZ basis, we see nothing. *click*

It is easy to understand why this happens: since the XYZ CMFs never overlap the 350nm range, the part of the re-radiation matrix that can absorb and re-radiate this part of the spectrum is unaccounted for during the reduction. *click*

To mitigate this, we can add an additional function to the CMFs that covers the UV range. Using it, we account for the missing energy. But now we have to use a fourth channel and 4x4 matrices during light transport. If we had used another set of 3 basis functions for the reduction, we would have lost accuracy for the visible range. So, selecting the basis is a trade-off between how faithful we want to be and how much computation we can afford. *click*

Reduction and Light Transport

How to use reduced matrices in path tracing?
- This is a form of vector light transport [Jarabo and Arellano 2017]
- The importance (adjoint of radiance) is a matrix

$T = \begin{bmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$

$T_1 = T \times R$

$\mathbf{c} = T_n \times \mathbf{l}$

[Jarabo and Arellano 2017]

So far so good it seems. Well, I haven't covered the case of how to use fluorescence in RGB path tracers. While direct illumination simply requires us to change a component-wise multiplication by a matrix multiplication, multiple bounces of light needs another change in a renderer's architecture. *click*

The point being that RGB path tracing is a form of vector-light transport. And while we usually do not account for it in practice, we have to be mindful about it here. For those interested by the details of what I am going to talk about, please refer to this great article by Jarabo and Arellano. *click*

We need to account for the fact that importance (the adjoint of radiance, a.k.a. throughput) is no longer a vector, but a matrix. And it makes sense when we think that a radiance triplet has no information on how its red component is going to affect say the blue component of the pixel. In practice, what we need to do is to start our eye paths with a throughput matrix and at each interaction, we accumulate the reduced material matrix to this throughput matrix. When we want to connect to the light, we multiply the throughput matrix with the light vector to get the path's color. *click*

Reduction and Light Transport

How to use reduced matrices in path tracing?
- This is a form of vector light transport [Jarabo and Arellano 2017]
- The importance (adjoint of radiance) is a matrix

Change ray payload to store matrices

RGB Rendering - Reduced

Spectral Rendering

RGBU Rendering - Reduced

Authoring Assets

What workflow to texture fluorescence?
- Can't paint with reduced matrices
- Not one workflow, depends on usage

Authoring Assets: Black Light

Requires an RGBU rendering pipe

Model the re-radiation as a separable function

$$ = $$

$$ \times $$

Reradiation

Absorption

Emission

$$ \mathcal{R}(\lambda_i, \lambda_o) = \mathcal{A}(\lambda_i) \times \mathcal{E}(\lambda_o) $$

Authoring Assets: Black Light

Requires an RGBU rendering pipe

Model the re-radiation as a separable function
- Reduction is split
- See our jupyter notebook

$$ \mathcal{R}(\lambda_i, \lambda_o) = \mathcal{A}(\lambda_i) \times \mathcal{E}(\lambda_o) $$

$$ R_{jk} = \int \mathcal{A}(\lambda_i) \tilde{s}_{j}(\lambda_i) \mbox{d}\lambda_i \times \int \mathcal{E}(\lambda_o) s_{k}(\lambda_o) \mbox{d}\lambda_o $$

$$ R =\mathbf{a} \times \mathbf{e}^T $$

Authoring Assets: Black Light

Requires an RGBU rendering pipe

Model the re-radiation as a separable function
- Reduction is split

Albedo: #ffffff

UV Fluo: #000000

Authoring Assets: Parametric Model

Using a palette interface
- Exposes the parametric model's parameters

Reradiation

Palette - illuminant E

Rendering

Fluo strength

Albedo

Arguably, the black light parameterization is a bit simple. To get finer control of fluorescence, we can use a parameteric model of fluorescence. Using such a model, we can build different ways to control the appearance. The first we provide is what we call a fluorescent palette. *click*

In essence, we abstract the handling of a material's parameters by displaying the achievable colors for a given illuminant. *click*

First, the artist must select the absorption band. A broadband will provide fluorescence for all types of illuminants, while a narrowband will select specific illuminants. *click*

Once the absorption band is selected, we display a set of reachable colors for a target illuminant (here E). The user can then select what color they want to display. *click*

This color is effectively what a rendering with the same illuminant produces. Changing the albedo or the absorption band updates the palette to display the landscape the user can reach. *click*

Authoring Assets: Parametric Model

Expose the parameters directly
- Pros: easy to map textures
- Cons: unintuitive editing mode

illuminant E

illuminant UV

A second option is to provide artists with control over the model's parameters. For each parameter, we can map the [0, 1] interval to match the range of meaningful values. *click*

We experimented with this design inside Gratin, a node-based shader writer. Here is a graph that maps a texture of fingerprints to the absorption mean. *click*

When used, depending on the absorption mean value in the texture, the fluorescent pattern can appear if the absorption's mean is within the light footprint. For example when this value is too high, UV light will not be absorbed and the pattern will not appear. But it will appear for white or daylight illuminants. The downside of such a method is that it requires artist training to understand the model's different parameters. *click*

Authoring Assets: Optimization Based

Provide a target appearance
- Per pixel optimization to obtain parameters
- Starting point: albedo, no fluorescence

3D model

target appearance for D65

target appearance for 450nm

Fluorescence strength

Albedo

Rendering

artist painted

per-pixel optimized

Storing & Filtering Fluorescence

Storing fluorescence
- Reduced RGB matrices → 9 floating point values
- Alternative: store and manipulate RGB triplets / parametric space

Filtering or interpolating fluorescence
- Use the reduced matrix for interpolation and filtering

Beyond Fluorescence

Reduction is a framework for converting spectral appearances
- Spectral reflectances, iridescence, ...
- Appearance models are most of the time linear operators

Example: Albedo Matrices

What if we reduce spectral reflectances?

$$ R_{kl} = \iint {\color{green} s_k(\lambda_i)} \; {\color{orange} \rho(\lambda_i) \delta(\lambda_i-\lambda_o) } \; {\color{green} \tilde{s}_l(\lambda_i)} \; \mbox{d}\lambda_i\; \mbox{d}\lambda_o $$

$$ R_{kl} = \int {\color{green} s_k(\lambda_i)} \; {\color{orange} \rho(\lambda_i) } \; {\color{green} \tilde{s}_l(\lambda_i)} \; \mbox{d}\lambda_i $$

$${\color{orange} \rho(\lambda) }$$

$$\mathcal{R}(\lambda_i, \lambda_o) = {\color{orange} \rho(\lambda_i) \delta(\lambda_i-\lambda_o) }$$

diagonal only

Example: Albedo Matrices

What if we reduce spectral reflectances?

What do we gain compared to vector albedo?
- Way to acheive metamerism without spectral

$light$ $[1,1,1]$ $[0.4,0.5,1]$

Example: Albedo Matrices

What if we reduce spectral reflectances?

What do we gain compared to vector albedo?
- Way to acheive metamerism without spectral
- Avoids locus degeneration for multiple scattering

spectral reference

vector albedo

albedo matrix

Another property of re-radiation matrices is that they avoid being trapped in the locus of RGB when they are used in multiple scattering. *click*

As an example, here is what happens when an RGB albedo is used in a participating medium or a surface where light bounces many, many times before reaching the eye. I am displaying the chromaticity of the reflected light after a varying number of bounces. The XYZ chromatic horseshoe is given as color reference. The curve starts at one bounce illumination and continues with a hundred of them. What we see is that the reflected color slowly turns to one of the corners of the chromaticity space. This is expected as only the maximum values of the RGB triplet will dominate after many bounces. *click*

This behavior is, however, not expected if we use the spectra that generated this RGB triplet. With a spectral albedo, after many bounces, the resulting color should converge toward one point on the chromatic horseshoe (in black). It is the chromaticity curve of monochromatic spectra. *click*

Now, if we do the same experiment but with reduced matrices instead of RGB albedo, we obtain a behavior much closer to the spectral reference. This is due to the fact that as scattering order increase, the resulting color will approach the first eigenvector of the reduced matrix, avoiding the corner of the chromaticity space. *click*

RGB Workflow for Spectral Effects

Can we author albedo matrices in RGB?
- Upscale an albedo vector with the dual basis
- Reduce to a 3D tensor product
- Re-align data with respect to the white point!

$${\color{orange} \rho(\lambda) }$$

⮕

✘

$$ \sum_k {\color{red}\rho_k } \, {s}_k(\lambda)$$

⬅

⭣

$$ R_{i,j} = \int {\color{green} s_i(\lambda)} \; {\color{orange} \rho(\lambda) } \; {\color{green} \tilde{s}_j(\lambda)} \; \mbox{d}\lambda $$

$$ R_{i,j} =\int {\color{green} s_i(\lambda)} \; {\color{red} \left[ \sum_k\rho_k \; {s}_k(\lambda)\right] } \; {\color{green} \tilde{s}_j(\lambda) } \; \mbox{d}\lambda $$

upscale

$$ R_{i,j} = {\color{red} \sum_k\rho_k }\int {\color{green} s_i(\lambda)} \; {\color{red} {s}_k(\lambda) } \; {\color{green} \tilde{s}_j(\lambda)} \; \mbox{d}\lambda $$

$$ R_{i,j} = \sum_k {\color{red} \rho_k} \; { \color{orange} S_{i,j,k} } $$


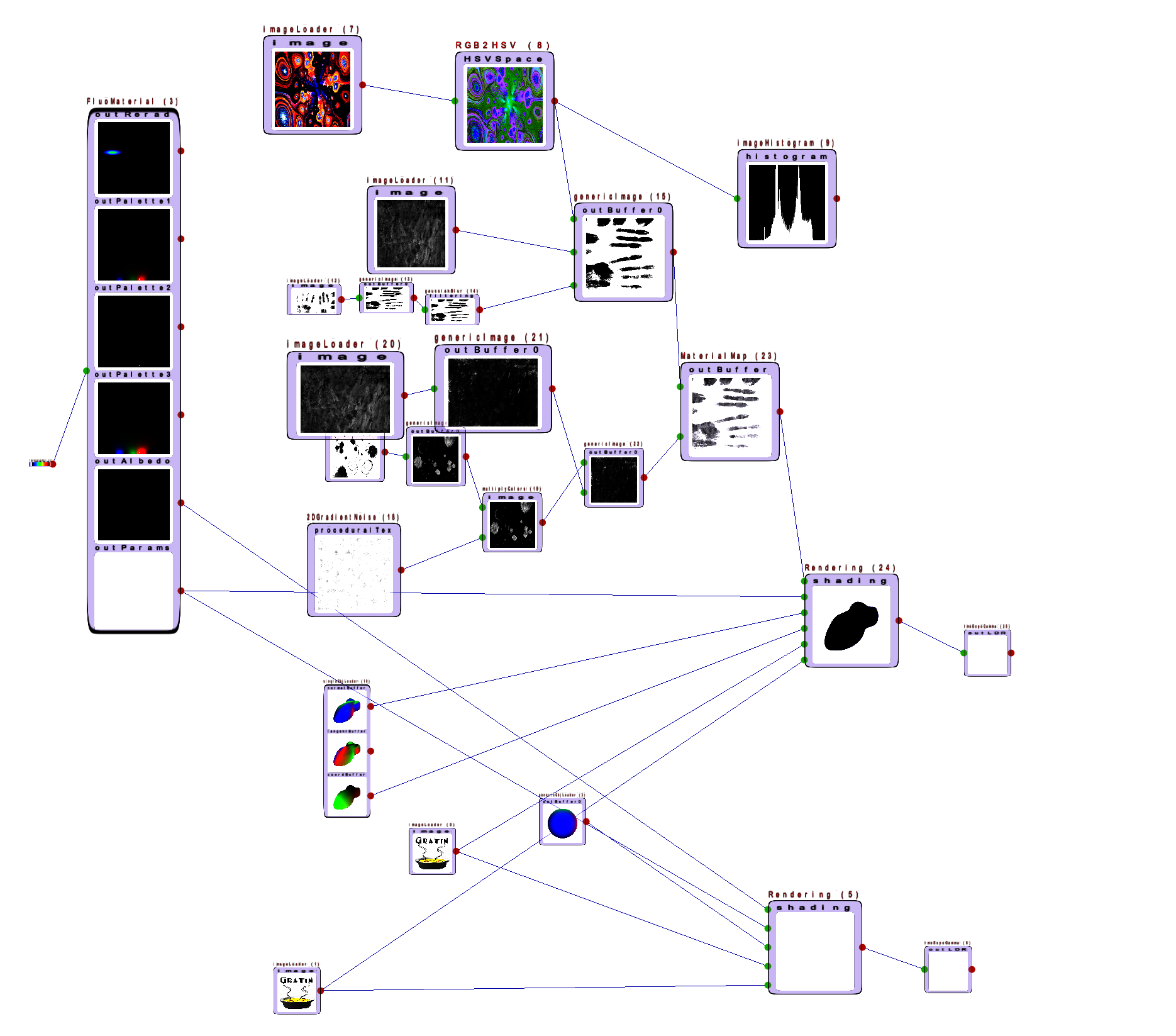
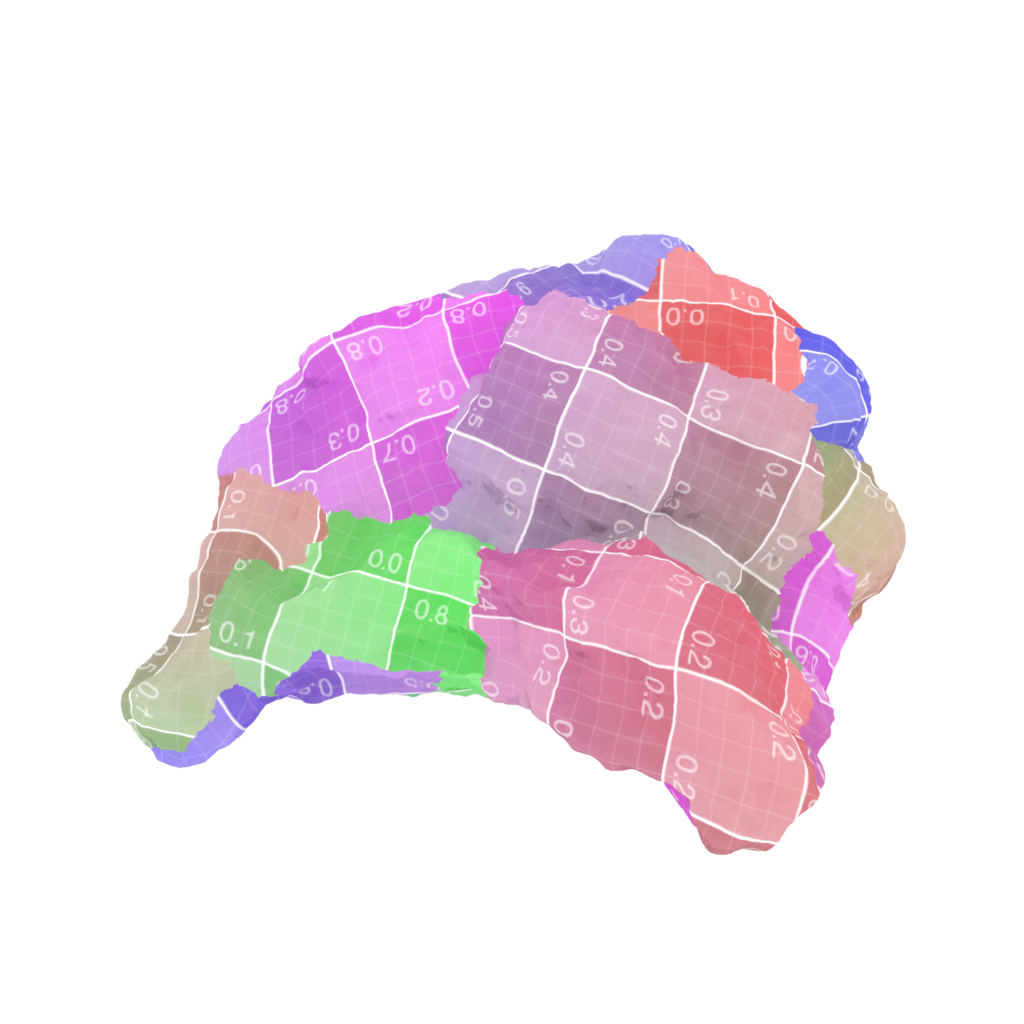
						def MatrixFromVector(r : Vector):
						# Build a 3D tensor from a triplet basis (3 x 3 x 3)
						R = np.concatenate([
										(S.T @ np.diag(S[:,0]) @ Sb)[..., None],
										(S.T @ np.diag(S[:,1]) @ Sb)[..., None],
										(S.T @ np.diag(S[:,2]) @ Sb)[..., None]
							], axis=-1)
						return R @ r

That's all good, but we probably do not want to rely on spectra to drive an RGB rendering pipeline, do we? *click*

What we need is a way to specify reduced matrices. *click*. So far, we have specified them using spectral data. *click* But what can we do if we don't have access to spectral data? *click* What we can rely on is a spectral upscaling method using the CMFs. *click*

Using a linear combination of the CMFs even simplifies the expression of the reduced matrix. *click* We can precompute a 3D tensor and use its product with a color triplet to obtain a reduced matrix. *click* Here is a code snippet showing how to precompute this tensor in Python and evaluate the reduced matrix from a triplet. Here S and Sb are the CMFs and their duals. *click*

Beware, however, that this transform does not fully preserve the input color. For that we need to re-align the input data with respect to the white point. We cover this transformation in our supplemental Jupyter notebook. Please check it out for further details. *click*

RGB Workflow for Spectral Effects

Can we author albedo matrices in RGB?
- Upscale an albedo vector with the dual basis
- Reduce to a 3D tensor product
- Re-align data with respect to the white point!

This upsampling avoids chroma locus

No metamerism yet!

vector -

spectral -

matrix -

vector -

spectral -

matrix -

vector -

spectral -

matrix -

saturate to wrong color

darken fast

Design Metamers in RGB+UV

Metameric blacks [Wyszecki 1958] of reduced matrices
- Spectra/Matrices as a sum
- with non-contributing components

$$ \times\; \mathbf{l} $$

$$ = $$

$$ \times\; \mathbf{l} $$

$$ + $$

$$ \times\; \mathbf{l} $$

if $R \times \mathbf{l} = [0, 0, 0]$ $R$ is a metameric black

Design Metamers in RGB+UV

Metameric blacks [Wyszecki 1958] of reduced matrices
- Spectra/Matrices as a sum
- with non-contributing components

How can we generate metameric black matrices?
- Vectors of $R_b$ are orthogonal to $\mathbf{l}$

$$ R_b \times \mathbf{l} = \mathbf{0} \rightarrow R_b^k \cdot \mathbf{l} = 0 \; \forall k$$

Design Metamers in RGB+UV

$+$

$light$ $[1,1,1]$ $[0.4,0.5,1]$

Design Metamers in RGB+UV

Metameric blacks [Wyszecki 1958] of reduced matrices
- Spectra/Matrices as a sum
- with non-contributing components

How can we generate metameric black matrices?
- Vectors of $R_b$ are orthogonal to $\mathbf{l}$

Still some open research problems
- How to control this space?
- What are the associated metameric black spectra?

Summary

Fluorescence is a new tool for shading design
- Enables new appearances
- Works with both RGB and spectral render pipelines
- Now with tools for authoring workflows

Reduced matrices improve legacy RGB
- Bring spectral effects in (metamerism, multiple scattering, ...)

Goal: create a continuum between render pipelines

Spectral Rendering in a Non-Spectral Renderer: How Can we Author and Render Fluorescence in RGB?

More Fluorescence

Fluorescence

Physics of Fluorescence

Physics of Fluorescence

Physically based Fluorescence

Spectral Rendering with Fluorescence

RGB Rendering with Fluorescence

Spectral Reduction of Fluorescence

Spectral Reduction of Fluorescence

Spectral Reduction: Example on Measured Data

Spectral Reduction: Example on Measured Data

Spectral Reduction: Basis

Reduction and Light Transport

Reduction and Light Transport

Authoring Assets

Authoring Assets: Black Light

Authoring Assets: Black Light

Authoring Assets: Black Light

Authoring Assets: Parametric Model

Authoring Assets: Parametric Model

Authoring Assets: Optimization Based

Storing & Filtering Fluorescence

Beyond Fluorescence

Example: Albedo Matrices

Example: Albedo Matrices

Example: Albedo Matrices

RGB Workflow for Spectral Effects

RGB Workflow for Spectral Effects

Design Metamers in RGB+UV

Design Metamers in RGB+UV

Design Metamers in RGB+UV

Design Metamers in RGB+UV

Summary

Thank You!

Spectral Rendering in a Non-Spectral Renderer:
How Can we Author and Render Fluorescence in RGB?