Perpendicular Possibilities
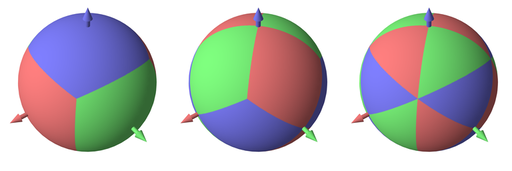
Figure 1: Major axes for original (left), swizzle (mid) and perpendicular (right) vectors.
Introduction
Two months ago, there was a question (and subsequent discussion) on Twitter as to how to go about generating a perpendicular unit vector, preferably without branching. It seemed about time that I finally post something more complete on the subject, since there are various ways to go about doing this, as well as a few traps awaiting the unwary programmer.
Solution Quartet
Here are four options with various trade-offs. If you happen to know of any others, by all means let me know and I’ll update this post.
Note: in all of the following approaches, normalisation is left as an optional post-processing step.
Quick ’n’ Dirty
A quick hack involves taking the cross product of the original unit vector – let’s call it $\mathbf{u}(x, y, z)$ – with a fixed ‘up’ axis, e.g. $(0, 1, 0)$, and then normalising. A problem here is that if the two vectors are very close – or equally, pointing directly away from each other – then the result will be a degenerate vector. However, it’s still a reasonable approach in the context of a camera, if the view direction can be restricted to guard against this. A general solution in this situation is to fall back to an alternative axis:
1vec3 perp_quick(vec3 u)
2{
3 vec3 v;
4 if (abs(u.y) < 0.99) // abs(dot(u, UP)), somewhat arbitrary epsilon
5 v = vec3(-u.z, 0, u.x); // cross(u, UP)
6 else
7 v = vec3(0, u.z, -u.y); // cross(u, RIGHT)
8 return v;
9}Hughes-Möller
In a neat little Journal of Graphics Tools paper [1], Hughes and Möller proposed a more systematic approach to computing a perpendicular vector. Here’s the heart of it:
$$\mathbf{\bar{v}} = \begin{cases} (\;\;\:0,-z,\;\;\; y) & \text{if } |x| < |y| \text{ and } |x| < |z| \\ (-z,\;\;\;0,\;\;\, x) & \text{if } |y| < |x| \text{ and } |y| < |z| \\ (-y,\;\;\,x,\;\;\; 0) & \text{if } |z| < |x| \text{ and } |z| < |y| \\ \end{cases}.$$Or, as the paper also states: “Take the smallest entry (in absolute value) of $\mathbf{u}$ and set it to zero; swap the other two entries and negate the first of them”.

Figure 2: Distribution of $\mathbf{\bar{v}}$ over the sphere.
However, there’s a problem with this as written: it doesn’t handle cases where multiple components are the smallest, such as $(0, 0, 1)$. I hit this a few years back when I needed to generate an orthonormal basis for some offline geometry processing, and it’s easily remedied by replacing $<$ with $\leq$. Here’s a corrected version in code form:
1vec3 perp_hm(vec3 u)
2{
3 vec3 a = abs(u);
4 vec3 v;
5 if (a.x <= a.y && a.x <= a.z)
6 v = vec3(0, -u.z, u.y);
7 else if (a.y <= a.x && a.y <= a.z)
8 v = vec3(-u.z, 0, u.x);
9 else
10 v = vec3(-u.y, u.x, 0);
11 return v;
12}Stark
More recently, Michael M. Stark suggested some improvements to the Hughes-Möller approach [2]. Firstly, his choice of permuted vectors is almost the same – differing only in signs – but even easier to remember:
$$ \mathbf{\bar{v}} = \begin{pmatrix} x \\ y \\ z \end{pmatrix} \times \begin{pmatrix} \left[x \text{ is smallest}\right] \\ \left[y \text{ is smallest}\right] \\ \left[z \text{ is smallest}\right] \end{pmatrix}. $$In plain English: the perpendicular vector $\mathbf{\bar{v}}$ is found by taking the cross product of $\mathbf{u}$ with the axis of its smallest component. (Note: the same care is needed when multiple components are the smallest.)
Figure 3 visualises this intermediate ‘swizzle’ vector over the sphere:

Figure 3: Intermediate swizzle vector.
Secondly, Michael also provides a branch-free implementation:
1vec3 perp_stark(vec3 u)
2{
3 vec3 a = abs(u);
4 uint uyx = SIGNBIT(a.x - a.y);
5 uint uzx = SIGNBIT(a.x - a.z);
6 uint uzy = SIGNBIT(a.y - a.z);
7
8 uint xm = uyx & uzx;
9 uint ym = (1^xm) & uzy;
10 uint zm = 1^(xm & ym);
11
12 vec3 v = cross(u, vec3(xm, ym, zm));
13 return v;
14}I know what you’re thinking, there’s a problem here too: it should be zm = 1^(xm | ym)! Although still robust, the effect of this error is that the nice property of even, symmetrical distribution over the sphere is lost:

Figure 4: Broken symmetry in the perpendicular vector.
XNAMath
Finally, another branch-free solution is provided in the form of XMVector3Orthogonal, which is part of the XNAMath library. Here’s the actual code taken from the DirectX SDK (June 2010):
1XMFINLINE XMVECTOR XMVector3Orthogonal(FXMVECTOR V)
2{
3 XMVECTOR NegativeV;
4 XMVECTOR Z, YZYY;
5 XMVECTOR ZIsNegative, YZYYIsNegative;
6 XMVECTOR S, D;
7 XMVECTOR R0, R1;
8 XMVECTOR Select;
9 XMVECTOR Zero;
10 XMVECTOR Result;
11 static CONST XMVECTORU32 Permute1X0X0X0X =
12 {XM_PERMUTE_1X, XM_PERMUTE_0X, XM_PERMUTE_0X, XM_PERMUTE_0X};
13 static CONST XMVECTORU32 Permute0Y0Z0Y0Y =
14 {XM_PERMUTE_0Y, XM_PERMUTE_0Z, XM_PERMUTE_0Y, XM_PERMUTE_0Y};
15
16 Zero = XMVectorZero();
17 Z = XMVectorSplatZ(V);
18 YZYY = XMVectorPermute(V, V, Permute0Y0Z0Y0Y.v);
19
20 NegativeV = XMVectorSubtract(Zero, V);
21
22 ZIsNegative = XMVectorLess(Z, Zero);
23 YZYYIsNegative = XMVectorLess(YZYY, Zero);
24
25 S = XMVectorAdd(YZYY, Z);
26 D = XMVectorSubtract(YZYY, Z);
27
28 Select = XMVectorEqualInt(ZIsNegative, YZYYIsNegative);
29
30 R0 = XMVectorPermute(NegativeV, S, Permute1X0X0X0X.v);
31 R1 = XMVectorPermute(V, D, Permute1X0X0X0X.v);
32
33 Result = XMVectorSelect(R1, R0, Select);
34
35 return Result;
36}Let me save you the trouble of parsing this fully (or consider it an exercise for later); if you boil it down, what you’re effectively left with is:
$$ \mathbf{\bar{v}} = \begin{pmatrix}x\\y\\z\end{pmatrix} \times \begin{pmatrix}0\\-\mathrm{sign}(yz)\\1\end{pmatrix} \quad \text{where } \mathrm{sign}(x) = \begin{cases} \phantom{-}1 &\text{if } x \ge 0 \\ -1 & \text{otherwise} \end{cases}. $$I’ve failed, thus far, to pinpoint the origin of or thought process behind this approach. That said, some insight can be gained from visualising the resulting vectors:
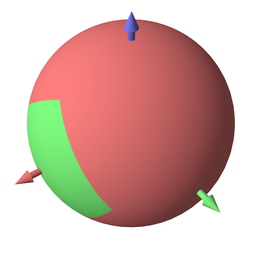
Figure 5: Covering one’s axis.
Their maximum component is in the x axis, except close to the +/-ve x poles. Essentially, Microsoft’s solution ensures robustness without concern for distribution, much like the initial ‘quick’ approach.
Performance
I haven’t benchmarked these implementations, since in cases where I’ve needed to generate perpendicular vectors, absolute speed wasn’t important or the call frequency was vanishingly small. Even in performance-critical situations, it really depends on what properties/restrictions you can live with and your target architecture(s). Still, I can’t help but think that XMVector3Orthogonal is doing a little bit more than it needs to, so maybe there’s cause to revisit this subject at a later date.
Conclusion
I hope you’ve learnt something about generating perpendicular vectors, or that I’ve at least made you aware of some of the minor issues in previous work on the subject. On that note, if you spot any new errors here, please let me know!
References
[1] Hughes, J. F., Möller, T., “Building an Orthonormal Basis from a Unit Vector”, Journal of Graphics Tools 4:4 (1999), 33-35.
[2] Stark, M. M., “Efficient Construction of Perpendicular Vectors without Branching”, Journal of Graphics Tools 14:1 (2009), 55-61.